
【题目】如图是一幅长为90cm,宽为60cm的有关北京东奥会的长方形宣传画.
(1)为测量宣传画上吉祥物冰墩墩的面积,现将宣传画平铺在地上,向长方形宣传画内随机投掷骰子(假设骰子落在长方形内的每一点都是等可能的),经过大量重复投掷试验,发现骰子落在吉祥物冰墩墩中的频率稳定在常数0.4附近,由此可估计宣传画上吉祥物冰墩墩的面积约为 cm2;
(2)若要为此宣传画配一个镜框制成一幅矩形挂画,要求镜框的四条边宽度相等.如果要使整个挂画的面积为7000cm2,那么镜框边的宽度应是多少厘米?

【答案】(1)2160;(2)镜框边的宽度应是5厘米.
【解析】
(1)利用频率估计概率得到估计骰子落在世界杯图案中的概率为0.4,然后根据几何概率的计算方法计算宣传画上吉祥物冰墩墩的面积即可;
(2)设镜框的宽度为xcm,表示出大长方形的长为90+2x,宽为60+2x,根据整幅作品(包括木框)的面积为7000cm2列出方程,解方程可得.
(1)∵骰子落在吉祥物冰墩墩中的频率稳定在常数0.4附近,
∴估计骰子落在骰子落在吉祥物冰墩墩中的概率为0.4,
∴估计宣传画上吉祥物冰墩墩的面积=0.4×(60×90)=2160(cm2).
故答案为:2160;
(2)设镜框的宽度为xcm,根据题意,得:
(60+2x)(90+2x)=7000,
整理,得:x2+75x﹣400=0,
即:(x+80)(x﹣5)=0,
解得:x=﹣80(舍)或x=5,
答:镜框边的宽度应是5厘米.


科目:初中数学 来源: 题型:
【题目】山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:
(1)每千克核桃应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF=![]() CD,下列结论中错误的是( )
CD,下列结论中错误的是( )
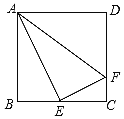
A.![]() B.△ABE∽△AEF
B.△ABE∽△AEF
C.△ABE∽△ECFD.△ADF∽△ECF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年的北京世园会在北京延庆区成功举办,这是我国举办的级别最高、规模最大的国际性博览会,吸引了各地的游客前来参观.会展期间延庆某宾馆有50间房供游客居住,当每间房每天定价为380元时,宾馆会住满;当每间房每天定价每增加20元时,就会空闲一间房,如果有游客居住,宾馆需对居住的每间房每天支出30元的费用,当房价定为多少元时,宾馆当天的利润为20250元?设房价比定价380元增加x元,则有( )
A.(x+380)(50﹣![]() )﹣50×30=20250
)﹣50×30=20250
B.(380+x﹣30)(50﹣![]() )=20250
)=20250
C.x(50﹣![]() )﹣50×30=20250
)﹣50×30=20250
D.(x﹣30)(50﹣![]() )=20250
)=20250
查看答案和解析>>
科目:初中数学 来源: 题型:
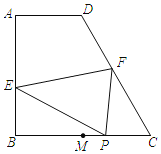
【题目】如图,已知AD∥BC,∠B=90°,∠C=60°,BC=2AD=4,点M为边BC的中点,点E、F在边AB、CD上运动,点P在线段MC上运动,连接EF、EP、PF,则△EFP的周长最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出
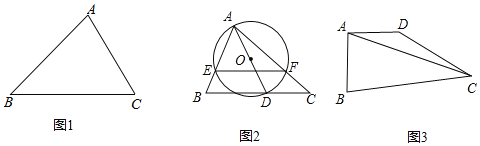
(1)如图1,在△ABC中,∠A=75°,∠C=60°,AC=6![]() ,求△ABC的外接圆半径R的值;
,求△ABC的外接圆半径R的值;
问题探究
(2)如图2,在△ABC中,∠BAC=60°,∠C=45°,AC=8![]() ,点D为边BC上的动点,连接AD以AD为直径作⊙O交边AB、AC分别于点E、F,接E、F,求EF的最小值;
,点D为边BC上的动点,连接AD以AD为直径作⊙O交边AB、AC分别于点E、F,接E、F,求EF的最小值;
问题解决
(3)如图3,在四边形ABCD中,∠BAD=90°,∠BCD=30°,AB=AD,BC+CD=12![]() ,连接AC,线段AC的长是否存在最小值,若存在,求最小值:若不存在,请说明理由.
,连接AC,线段AC的长是否存在最小值,若存在,求最小值:若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
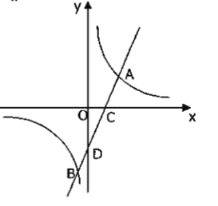
【题目】如图,已知点![]() ,
,![]() 在反比例函数
在反比例函数![]() 的图象上,直线
的图象上,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴相交于
轴相交于![]() 、
、![]() 两点.
两点.
(1)求直线![]() 的解析式:
的解析式:
(2)求![]() 、
、![]() 两点坐标;
两点坐标;
(3)连接![]() 、
、![]() ,记
,记![]() 的面积为
的面积为![]() 、
、![]() 面积为
面积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
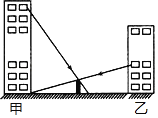
【题目】如图,在甲、乙两座楼正中间有一堵院墙,小明站在甲楼某层窗口前,同时小光站在乙楼某层窗口前观察这堵墙,小明视线所及位置如图所示,小光视线恰好落在甲楼底部.已知墙的高度为5米,两栋楼的间距为100米,小明视线所及位置到墙的距离为10米.
(1)请根据题意画出平面图形,并标上相应字母.
(2)求甲、乙两人的观测点到地面高度的距离差.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com