
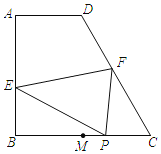
【题目】如图,已知AD∥BC,∠B=90°,∠C=60°,BC=2AD=4,点M为边BC的中点,点E、F在边AB、CD上运动,点P在线段MC上运动,连接EF、EP、PF,则△EFP的周长最小值为_____.
【答案】2![]() .
.
【解析】
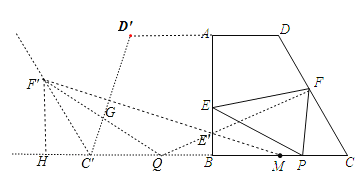
作梯形ABCD关于AB的轴对称图形,将 QC'绕点C'逆时针旋转60°,点Q的对应点为F',连接F'M,交C' D'于点G,交AB与点E',延长QE'交CD于点F,,则有GE'=FE',P与Q是关于AB的对称点,当点F'、G、P三点在一条直线上时,△FEP的周长最小即为F'G+GE'+E'P,此时点P与点M重合,F'M为所求长度;过点F'作F'H⊥BC',M是BC中点,则Q是BC'中点,由已知条件∠B=90°,∠C=60°,BC=2AD=4,可得C'Q=F'C'=2,∠F'C'H=60°,所以F'H=![]() ,HC'=7,在Rt△MF'H中,F'M=2
,HC'=7,在Rt△MF'H中,F'M=2![]() .
.
解:作梯形ABCD关于AB的轴对称图形,将 QC'绕点C'逆时针旋转60°,点Q的对应点为F',连接F'M,交C' D'于点G,交AB与点E',延长QE'交CD于点F,
则有GE'=FE',P与Q是关于AB的对称点,
∴PF=GQ,
又∵GF'=GQ,
∴当点F'、G、P三点在一条直线上时,△FEP的周长最小即为F'G+GE'+E'P,
此时点P与点M重合,
∴F'M为所求长度;
过点F'作F'H⊥BC',
∵M是BC中点,
∴Q是BC'中点,
∵∠B=90°,∠C=60°,BC=2AD=4,
∴C'Q=F'C'=2,∠F'C'H=60°,
∴F'H=![]() ,HC'=7,
,HC'=7,
在Rt△MF'H中,F'M=2![]() ;
;
∴△FEP的周长最小值为2![]() ;
;
故答案为2![]() ;
;


科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() ,与
,与![]() 轴相交于点
轴相交于点![]() ,过点C作
,过点C作![]() 轴,交抛物线于点
轴,交抛物线于点![]() .
.
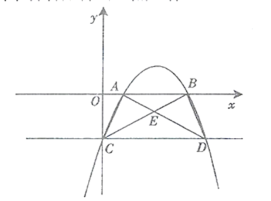
(1)求梯形ACDB的面积;
(2)若梯形ACDB的对角线![]() 交于点
交于点![]() ,求点
,求点![]() 的坐标,并求经过
的坐标,并求经过![]() 三点的抛物线的解析式; .
三点的抛物线的解析式; .
(3)点![]() 是射线
是射线![]() 上一点,且
上一点,且![]() 与
与![]() 相似,求符合条件的
相似,求符合条件的![]() 点坐标.
点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
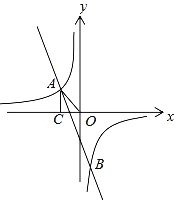
【题目】如图,一次函数y=kx+b的图象与反比例函数![]() 的图象相交于A(m,4)、B(2,﹣6)两点,过A作AC⊥x轴交于点C,连接OA.
的图象相交于A(m,4)、B(2,﹣6)两点,过A作AC⊥x轴交于点C,连接OA.
(1)分别求出一次函数与反比例函数的表达式;
(2)若直线AB上有一点M,连接MC,且满足S△AMC=3S△AOC,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一幅长为90cm,宽为60cm的有关北京东奥会的长方形宣传画.
(1)为测量宣传画上吉祥物冰墩墩的面积,现将宣传画平铺在地上,向长方形宣传画内随机投掷骰子(假设骰子落在长方形内的每一点都是等可能的),经过大量重复投掷试验,发现骰子落在吉祥物冰墩墩中的频率稳定在常数0.4附近,由此可估计宣传画上吉祥物冰墩墩的面积约为 cm2;
(2)若要为此宣传画配一个镜框制成一幅矩形挂画,要求镜框的四条边宽度相等.如果要使整个挂画的面积为7000cm2,那么镜框边的宽度应是多少厘米?

查看答案和解析>>
科目:初中数学 来源: 题型:
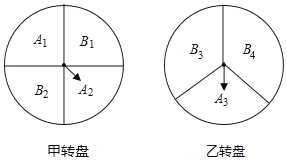
【题目】某超市在春节期间开展优惠活动,凡购物者可以通过转动转盘的方式享受折扣和优惠,在每个转盘中指针指向每个区域的可能性均相同,若指针指向分界线,则重新转动转盘,区域对应的优惠方式如下,A1,A2,A3区域分别对应9折8折和7折优惠,B1,B2,B3,B4区域对应不优惠?本次活动共有两种方式.
方式一:转动转盘甲,指针指向折扣区域时,所购物品享受对应的折扣优惠,指针指向其他区域无优惠;
方式二:同时转动转盘甲和转盘乙,若两个转盘的指针均指向折扣区域时,所购物品享受折上折的优惠,其他情况无优惠.
(1)若顾客选择方式一,则享受优惠的概率为 ;
(2)若顾客选择方式二,请用树状图或列表法列出所有可能顾客享受折上折优惠的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
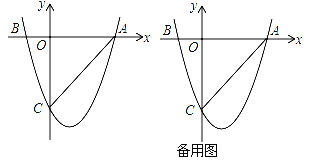
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴相交于点C(0,﹣3)
(1)求该二次函数的解析式;
(2)设E是y轴右侧抛物线上异于点A的一个动点,过点E作x轴的平行线交抛物线于另一点F,过点F作FG垂直于x轴于点G,再过点E作EH垂直于x轴于点H,得到矩形EFGH,则在点E的运动过程中,当矩形EFGH为正方形时,求出该正方形的边长;
(3)设P点是x轴下方的抛物线上的一个动点,连接PA、PC,求△PAC面积的取值范围,若△PAC面积为整数时,这样的△PAC有几个?
查看答案和解析>>
科目:初中数学 来源: 题型:
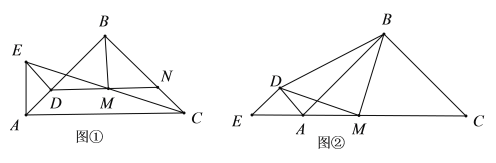
【题目】如图①,已知点![]() 在线段
在线段![]() 上,在
上,在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,
![]() ,且
,且![]() 为
为![]() 的中点.
的中点.
(1)连接![]() 并延长交
并延长交![]() 于
于![]() ,求证:
,求证:![]() ;
;
(2)直接写出线段![]() 与
与![]() 的关系: ;
的关系: ;
(3)若将![]() 绕点
绕点![]() 逆时针旋转,使点
逆时针旋转,使点![]() 在线段
在线段![]() 的延长线上(如图②所示位置),则(2)中的结论是否仍成立?若成立,请证明;若不成立,请说明理由.
的延长线上(如图②所示位置),则(2)中的结论是否仍成立?若成立,请证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋里装有4个大小、质地均相同的乒乓球,每个球上面分别标有1,2,3,4.小林先从布袋中随机抽取一个乒乓球(不放回去),再从剩下的3个球中随机抽取第二个乒乓球.
(1)请你用树状图或列表法列出所有可能的结果;
(2)求两次取得乒乓球的数字之积为奇数的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com