
【题目】如图,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() ,与
,与![]() 轴相交于点
轴相交于点![]() ,过点C作
,过点C作![]() 轴,交抛物线于点
轴,交抛物线于点![]() .
.
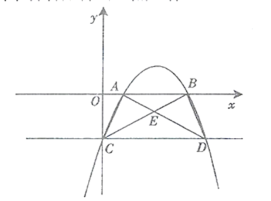
(1)求梯形ACDB的面积;
(2)若梯形ACDB的对角线![]() 交于点
交于点![]() ,求点
,求点![]() 的坐标,并求经过
的坐标,并求经过![]() 三点的抛物线的解析式; .
三点的抛物线的解析式; .
(3)点![]() 是射线
是射线![]() 上一点,且
上一点,且![]() 与
与![]() 相似,求符合条件的
相似,求符合条件的![]() 点坐标.
点坐标.
【答案】(1) ![]() ;(2)
;(2)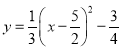 ;(3)
;(3) ![]() ,
,![]()
【解析】
(1)先求得点A、B、C、D的坐标,确定AB=3,CD=5,OC=2,再求梯形的面积即可;(2)根据对称性求得点E的横坐标,再利用平行线分线段成比例求得纵坐标,即可求过![]() 三点的抛物线的解析式;
三点的抛物线的解析式;
(3)由AB∥CD得∠ABC=∠BCP,当满足![]() ,或
,或![]() 时,
时,![]() 与
与![]() 相似,即可求得点P的坐标.
相似,即可求得点P的坐标.
(1)令![]() 中y=0,得
中y=0,得![]() ,
,
解得x1=1,x2=4,
∴![]() ,
,
∴AB=3,
令![]() 中x=0,得y=-2,
中x=0,得y=-2,
∴![]() ,
,
∵![]() 轴,
轴,
∴将y=-2代入![]() ,得
,得![]() ,
,
∴![]()
∴CD=5,
∴S梯形ACDB=![]() ;
;
(2)由抛物线的对称性有![]()
过![]() ,作
,作![]()
![]()
设过A、B、E三点的抛物线解析式为y=a(x-1)(x-4),将点E的坐标代入,得a=![]() ,
,
∴y=![]() (x-1)(x-4)=
(x-1)(x-4)=![]()
∴经过![]() 三点的抛物线的解析式为
三点的抛物线的解析式为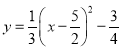 ;
;
(3) 点![]() 在
在![]() 的右侧,
的右侧,
①当∠CAB=∠CPB时,
∵![]() ∥
∥![]() ,
,
∴![]() ,
,
又∵BC=BC,
∴![]() ,
,
∴CP=AB=3,
∴P(3,-2);
②当∠CAB=∠CBP时,,
∵![]() ∥
∥![]() ,
,
∴![]() ,
,
∴△BCP∽△ABC,
∴![]() ,
,
∴![]()
得![]() ,
,
∴![]() ,
,
综上,P(3,-2)或![]() .
.


科目:初中数学 来源: 题型:
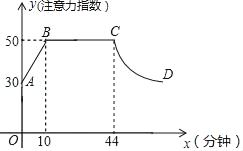
【题目】一般情况下,中学生完成数学家庭作业时,注意力指数随时间x(分钟)的变化规律如图所示(其中AB、BC为线段,CD为双曲线的一部分).
(1)分别求出线段AB和双曲线CD的函数关系式;
(2)若学生的注意力指数不低于40为高效时间,根据图中信息,求出一般情况下,完成一份数学家庭作业的高效时间是多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,E是BC上的一点,连接AE,过B点作BH⊥AE,垂足为点H,延长BH交CD于点F,连接AF.
(1)求证AE=BF;
(2)若正方形的边长是5,BE=2,求AF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
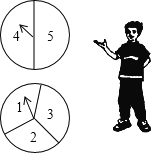
【题目】甲、乙两人用如图所示的两个分格均匀的转盘做游戏:分别转动两个转盘,转盘停止后,指针指向一个数字(若指针恰好停在分格线上,则重转一次),用所指的两个数字求和,如果和大于6,那么甲获胜;如果和不大于6,那么乙获胜.请你帮忙解决下列问题:
(l)利用树状图(或列表)的方法表示游戏所有可能出现的结果.
(2)求甲、乙两人获胜的概率,并说明游戏是否公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
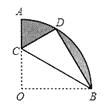
【题目】如图,在扇形OAB中,∠AOB=90°,半径OA=6.将扇形OAB沿过点B的直线折叠.点O恰好落在弧AB上点D处,折痕交OA于点C,求整个阴影部分的周长和面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中∠C=90°、∠A=30°,在AC边上取点O画圆使⊙O经过A、B两点,
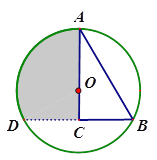
(1)求证:以O为圆心,以OC为半径的圆与AB相切.
(2)下列结论正确的序号是___________.(少选酌情给分,多选、错均不给分)
①AO=2CO ;
②AO=BC;
③延长BC交⊙O与D,则A、B、D是⊙O的三等分点.
④图中阴影面积为: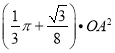
查看答案和解析>>
科目:初中数学 来源: 题型:
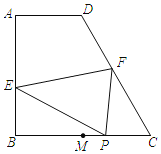
【题目】如图,已知AD∥BC,∠B=90°,∠C=60°,BC=2AD=4,点M为边BC的中点,点E、F在边AB、CD上运动,点P在线段MC上运动,连接EF、EP、PF,则△EFP的周长最小值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com