
【题目】已知二次函数的图象以![]() 为顶点,且过点
为顶点,且过点![]()
(1)求该函数的关系式;
(2)求该函数图象与坐标轴的交点坐标;
【答案】(1)![]() ;(2)该函数的图像与坐标轴的交点是
;(2)该函数的图像与坐标轴的交点是![]() ,
,![]() ,
,![]()
【解析】
(1)根据图象的顶点A(1,4)来设该二次函数的关系式,然后将点B代入,即用待定系数法来求二次函数解析式;
(2)令y=0,然后将其代入函数关系式,解一元二次方程即可,再令x=0,求出与y轴交点.
(1)由顶点A(1,4),可设二次函数关系式为y=a(x+1)2+4(a≠0).
∵二次函数的图象过点B(2,5),
∴点B(2,5)满足二次函数关系式,
∴5=a(2+1)2+4,
解得a=1.
∴二次函数的关系式是y=(x+1)2+4;
(2)令x=0,则y=(0+1)2+4=3,
∴图象与y轴的交点坐标为(0,3);
令y=0,则0=(x+1)2+4,
解得x1=3,x2=1,
故图象与x轴的交点坐标是(3,0)、(1,0).
答:图象与y轴的交点坐标为(0,3),与x轴的交点坐标是(3,0)、(1,0).


科目:初中数学 来源: 题型:
【题目】如图,某校教学楼AB的后面有一建筑物CD,当光线与地面的夹角是22时,
教学楼在建筑物的墙上留下高2m的影子CE;而当光线与地面的夹角是45时,教学楼顶A在地面上的影子F与墙角C有13m的距离(B、F、C在一条直线上).
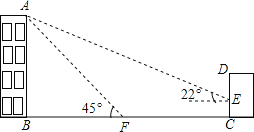
(1)求教学楼AB的高度;
(2)学校要在A、E之间挂一些彩旗,请你求出A、E之间的距离(结果保留整数).
(参考数据:sin22≈![]() ,cos22≈
,cos22≈![]() ,tan22≈
,tan22≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c中,b=4a,它的图象如图,有以下结论:①c>0;②a+b+c>0;③a﹣b+c>0 ④b2﹣4ac<0;⑤abc<0;⑥4a>c;其中正确的为_____(填序号).
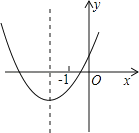
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在水果销售旺季,某水果店购进一优质水果,进价为20元/千克,售价不低于20元/千克,且不超过32元/千克,根据销售情况,发现该水果一天的销售量y(千克)与该天的售价x(元/千克)满足如下表所示的一次函数关系.

(1)某天这种水果的售价为23.5元/千克,求当天该水果的销售量.
(2)如果某天销售这种水果获利150元,那么该天水果的售价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() ,与
,与![]() 轴相交于点
轴相交于点![]() ,过点C作
,过点C作![]() 轴,交抛物线于点
轴,交抛物线于点![]() .
.
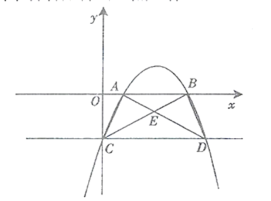
(1)求梯形ACDB的面积;
(2)若梯形ACDB的对角线![]() 交于点
交于点![]() ,求点
,求点![]() 的坐标,并求经过
的坐标,并求经过![]() 三点的抛物线的解析式; .
三点的抛物线的解析式; .
(3)点![]() 是射线
是射线![]() 上一点,且
上一点,且![]() 与
与![]() 相似,求符合条件的
相似,求符合条件的![]() 点坐标.
点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
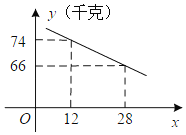
【题目】某片果园有果树80棵,现准备多种一些果树提高果园产量,但是如果多种树,那么树之间的距离和每棵树所受光照就会减少,单棵树的产量随之降低.若该果园每棵果树产果y(千克),增种果树x(棵),它们之间的函数关系如图所示.
(1)求y与x之间的函数关系式.
(2)在投入成本最低的情况下,增种果树多少棵时,果园可以收获果实7000千克.
(3)当增种果树多少棵时,果园的总产量w(千克)最大?此时每棵果树的产量是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果批发商销售每箱进价为40元的柑橘,物价部门规定每箱售价不得高于55元;市场调查发现,若每箱以45元的价格销售,平均每天销售105箱;每箱以50元的价格销售,平均每天销售90箱.假定每天销售量y(箱)与销售价x(元/箱)之间满足一次函数关系式.
(1)求平均每天销售量y(箱)与销售价x(元/箱)之间的函数关系式;
(2)求该批发商平均每天的销售利润w(元)与销售价x(元/箱)之间的函数关系式;
(3)当每箱苹果的销售价为多少元时,可以获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一幅长为90cm,宽为60cm的有关北京东奥会的长方形宣传画.
(1)为测量宣传画上吉祥物冰墩墩的面积,现将宣传画平铺在地上,向长方形宣传画内随机投掷骰子(假设骰子落在长方形内的每一点都是等可能的),经过大量重复投掷试验,发现骰子落在吉祥物冰墩墩中的频率稳定在常数0.4附近,由此可估计宣传画上吉祥物冰墩墩的面积约为 cm2;
(2)若要为此宣传画配一个镜框制成一幅矩形挂画,要求镜框的四条边宽度相等.如果要使整个挂画的面积为7000cm2,那么镜框边的宽度应是多少厘米?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com