
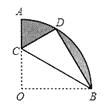
【题目】如图,在扇形OAB中,∠AOB=90°,半径OA=6.将扇形OAB沿过点B的直线折叠.点O恰好落在弧AB上点D处,折痕交OA于点C,求整个阴影部分的周长和面积.
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y=![]() 的图象交于A(2,3),B(﹣3,n)两点.
的图象交于A(2,3),B(﹣3,n)两点.
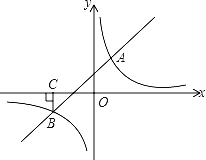
(1)求反比例函数的解析式;
(2)过B点作BC⊥x轴,垂足为C,若P是反比例函数图象上的一点,连接PC,PB,求当△PCB的面积等于5时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() ,与
,与![]() 轴相交于点
轴相交于点![]() ,过点C作
,过点C作![]() 轴,交抛物线于点
轴,交抛物线于点![]() .
.
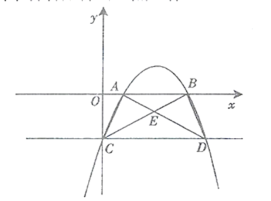
(1)求梯形ACDB的面积;
(2)若梯形ACDB的对角线![]() 交于点
交于点![]() ,求点
,求点![]() 的坐标,并求经过
的坐标,并求经过![]() 三点的抛物线的解析式; .
三点的抛物线的解析式; .
(3)点![]() 是射线
是射线![]() 上一点,且
上一点,且![]() 与
与![]() 相似,求符合条件的
相似,求符合条件的![]() 点坐标.
点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
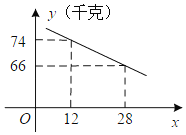
【题目】某片果园有果树80棵,现准备多种一些果树提高果园产量,但是如果多种树,那么树之间的距离和每棵树所受光照就会减少,单棵树的产量随之降低.若该果园每棵果树产果y(千克),增种果树x(棵),它们之间的函数关系如图所示.
(1)求y与x之间的函数关系式.
(2)在投入成本最低的情况下,增种果树多少棵时,果园可以收获果实7000千克.
(3)当增种果树多少棵时,果园的总产量w(千克)最大?此时每棵果树的产量是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣(2m﹣1)x+m2+1=0有两个不相等实数根x1,x2
(1)求实数m的取值范围;
(2)若x12+x22=x1x2+3时,求实数m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果批发商销售每箱进价为40元的柑橘,物价部门规定每箱售价不得高于55元;市场调查发现,若每箱以45元的价格销售,平均每天销售105箱;每箱以50元的价格销售,平均每天销售90箱.假定每天销售量y(箱)与销售价x(元/箱)之间满足一次函数关系式.
(1)求平均每天销售量y(箱)与销售价x(元/箱)之间的函数关系式;
(2)求该批发商平均每天的销售利润w(元)与销售价x(元/箱)之间的函数关系式;
(3)当每箱苹果的销售价为多少元时,可以获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
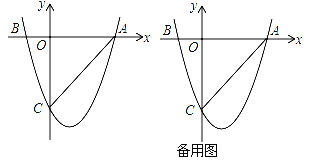
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴相交于点C(0,﹣3)
(1)求该二次函数的解析式;
(2)设E是y轴右侧抛物线上异于点A的一个动点,过点E作x轴的平行线交抛物线于另一点F,过点F作FG垂直于x轴于点G,再过点E作EH垂直于x轴于点H,得到矩形EFGH,则在点E的运动过程中,当矩形EFGH为正方形时,求出该正方形的边长;
(3)设P点是x轴下方的抛物线上的一个动点,连接PA、PC,求△PAC面积的取值范围,若△PAC面积为整数时,这样的△PAC有几个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com