
如图,在□ABCD中,过A、B、D三点的⊙O交BC于点E,连接DE,∠CDE=∠DAE.
(1)判断四边形ABED的形状,并说明理由;
(2)判断直线DC与⊙O的位置关系,并说明理由;
(3)若AB=3,AE=6,求CE的长.

(1)等腰梯形,理由见解析;(2)相切,理由见解析;(3) .
.
【解析】
试题分析:(1)四边形ABED为等腰梯形,理由为:利用四边形的外角等于它的内对角得到一对角相等,再由平行四边形的对角相等,利用等量代换得到∠DEC=∠C,利用等角对等边得到DE=DC,而DC=AB,故DE=AB,再由BE与AD平行,DE与AB不平行即可得证;
(2)DC与圆O相切,理由:连接DO并延长与圆交于F点,利用圆周角定理及等量代换得到OD与DC垂直,即可得证;
(3)由等腰梯形对角线相等得到AE=BD,利用弦切角等于夹弧所对的圆周角,以及公共角相等得到三角形CDE与三角形BCD相似,由相似得比例,即可求出CE的长.
试题解析:(1)四边形ABED是等腰梯形.
理由如下:在□ABCD中,AD∥BC,
∴∠DAE=∠AEB.
∴ ,DE=AB.
,DE=AB.
∵AB∥CD,∴AB与DE不平行.
∴四边形ABDE是等腰梯形.
(2)直线DC与⊙O相切.
如图,作直径DF,连接AF.于是,∠EAF=∠EDF.

∵∠DAE=∠CDE,
∴∠EAF+∠DAE=∠EDF+∠CDE,即∠DAF=∠CDF.
∵DF是⊙O的直径,点A在⊙O上,
∴∠DAF=90°,∴∠CDF=90°.∴OD⊥CD.
直线DC经过⊙O半径OD外端D,且与半径垂直,
直线DC与⊙O相切.
(3)由(1),∠EDA=∠DAB.
在□ABCD中,∠DAB=∠DCB,
∴∠EDA=∠DCB.又∵∠DAE=∠CDE,
∴△ADE∽△DCE.
∴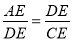 ,
,
∵AB=3,由(1)得,AB=DE=DC=3.
即 .
.
解得,CE= .
.
考点:1.切线的判定;2.平行四边形的性质.


科目:初中数学 来源:2013-2014学年江苏省扬州市邗江区九年级中考一模数学试卷(解析版) 题型:填空题
如图,以点P(2,0)为圆心, 为半径作圆,点M(a,b) 是⊙P上的一点,则
为半径作圆,点M(a,b) 是⊙P上的一点,则 的最大值是 .
的最大值是 .

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省张家港市九年级5月网上阅卷适应性考试数学试卷(解析版) 题型:选择题
已知∠1与∠2互补,并且∠1比∠2的3倍还大20°,若设∠1=x°,∠2=y°,则x、y满足的方程组为
A.  B.
B.
C. D.
D.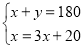
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省常州市九年级中考一模数学试卷(解析版) 题型:填空题
江苏省的面积约为102 600km2,这个数据用科学记数法可表示为 km2.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省常州市九年级中考一模数学试卷(解析版) 题型:选择题
甲、乙、丙、丁四位选手各10次射击成绩的平均数和方差如下表:
选 手 | 甲 | 乙 | 丙 | 丁 |
平均数(环) | 9.2 | 9.2 | 9.2 | 9.2 |
方差(环2) | 0.035 | 0.015 | 0.025 | 0.027 |
则这四人中成绩发挥最稳定的是( )
A.甲 B.乙 C.丙 D.丁
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省宜兴市和桥学区九年级下学期期中考试(一模)数学试卷(解析版) 题型:解答题
为了解某校九年级学生体育测试成绩情况,现从中随机抽取部分学生的体育成绩统计如下,其中右侧扇形统计图中的圆心角α为36°.

根据上面提供的信息,回答下列问题:
(1)m= ;抽取部分学生体育成绩的中位数为 分;
(2)已知该校九年级共有500名学生,如果体育成绩达33分以上(含33分)为优秀,请估计该校九年级学生体育成绩达到优秀的总人数.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省宜兴市和桥学区九年级下学期期中考试(一模)数学试卷(解析版) 题型:填空题
如图,将△ABC沿它的中位线MN折叠后,点A落在点A′处,若∠A=28°,∠B=130°,则∠A′NC= °.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省九年级新课结束考试数学试卷(解析版) 题型:解答题
如图,在△ABC中,∠C=90°,BC=5米,AC=12米.M点在线段CA上,从C向A运动,速度为1米/秒;同时N点在线段AB上,从A向B运动,速度为2米/秒.运动时间为t秒.

(1)当t为何值时,∠AMN=∠ANM?
(2)当t为何值时,△AMN的面积最大?并求出这个最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com