
����Ŀ����ͼ��������y=ax2��5ax��6a��x����A��B���㣨A��B�ң�����y���ڵ�C��ֱ��y=��x+b����������D����x����E���ҡ�ACE�����Ϊ6��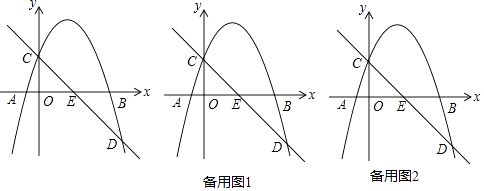
��1���������ߵĽ���ʽ��
��2����PΪCD�Ϸ���������һ�㣬����P��x���ƽ���ߣ���ֱ��CD��F����P��ĺ�����Ϊm���߶�PF�ij�Ϊd����d��m�ĺ�����ϵʽ��
��3���ڣ�2���������£�����P��PG��CD������ΪG������APG=��ACO�����P�����꣮
���𰸡�
��1��
�⣺��y=0����y=ax2��5ax��6a�ã�ax2��5ax��6a=0��
��a��x��6����x+1��=0��
��x=6��x=��1��
��A����1��0����B��6��0��
��y=0����y=��x+b�ã���x+b=0����ã�x=b����x=0����y=x+b�ã�y=b��
��OC=b��AE=b+1��
��S��ACE= ![]() b��b+1��=6��
b��b+1��=6��
��ã�b=3��b=��4����ȥ����
��C��0��3����
����C��������������ߵĽ���ʽ�ã���6a=3�����a=�� ![]() ��
��
�������ߵĽ���ʽΪy=�� ![]() x2+
x2+ ![]() x+3��
x+3��
��2��
�⣺��b=3��
��ֱ��CE�Ľ���ʽΪy=��x+3��
��P��m���� ![]() m2+
m2+ ![]() m+3����
m+3����
��PF��x�ᣬ
���F���������� ![]() m2+
m2+ ![]() m+3��
m+3��
�ੁx+3=�� ![]() m2+
m2+ ![]() m+3��
m+3��
��x= ![]() m2��
m2�� ![]() m��
m��
��d=PF=m���� ![]() m2��
m2�� ![]() m��=��
m��=�� ![]() m2+
m2+ ![]() m��
m��
��3��
�⣺��ͼ1��ʾ��
��OA=1��OC=3��
��tan��ACO= ![]() ��
��
�ߡ�APG=��ACO��
��tan��APG= ![]() ��
��
��ͼ1��ʾ������P��PC��x�ᣬ����ΪN������A��AM��PG������ΪM��
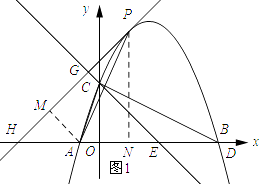
��OC=OE����COE=90�㣬
���CEO=45�㣮
�֡ߡ�EGH=90�㣬
���GHO=45�㣮
���AMHΪ����ֱ�������Σ�
��MH=AM=a��
��AH= ![]() a��PH=4a��
a��PH=4a��
��Rt��PHN��PN=AN=2 ![]() a��
a��
��AN= ![]() a��
a��
��tan��PAN=2��
��P��m���� ![]() m2+
m2+ ![]() m+3������PN=��
m+3������PN=�� ![]() m2+
m2+ ![]() m+3��AN=m+1����
m+3��AN=m+1���� ![]() =2��
=2��
��ã�m=��1����ȥ����m=2��
��P��2��6����
��ͼ2��ʾ������P��PC��x�ᣬ����ΪN������A��AM��PG������ΪM��
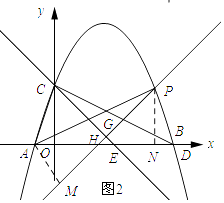
��AM=a����MP=3a��
��OC=OE����COE=90�㣬
���CEO=45�㣮
�֡ߡ�EGH=90�㣬
���GHO=45�㣮
���AMHΪ����ֱ�������Σ�
��MH=AM=a��
��AH= ![]() a��PH=2a��
a��PH=2a��
��Rt��PHN��PN=AN= ![]() a��
a��
��AN=2 ![]() a��
a��
��tan��PAN= ![]() ��
��
�� ![]() =
= ![]() ����ã�m=��1��m=5��
����ã�m=��1��m=5��
��P��5��3����
������������P������ΪP��2��6����P��5��3����
����������1����y=0���������ߵĽ���ʽ����÷��̵Ľ⣬�Ӷ��ɵõ���A�͵�B�����꣬Ȼ�����ݡ�ACE�����Ϊ6�����b��ֵ��Ȼ��ɵõ���C�����꣬�ʴ˿ɵõ�a��ֵ����2��ֱ��CE�Ľ���ʽΪy=��x+3����P��m���� ![]() m2+
m2+ ![]() m+3����Ȼ�����õ�F�ĺ����꣬�������d=PF�ɵõ�d��m�ĺ�����ϵʽ����3������P��PC��x�ᣬ����ΪN������A��AM��PG������ΪM��Ȼ��֤����AMH�͡�PHN��Ϊ����ֱ�������Σ���MH=AM=a��Ȼ������PN��AN�ij����ʴ˿ɵõ�tan��PAN=2��tan��PAN=
m+3����Ȼ�����õ�F�ĺ����꣬�������d=PF�ɵõ�d��m�ĺ�����ϵʽ����3������P��PC��x�ᣬ����ΪN������A��AM��PG������ΪM��Ȼ��֤����AMH�͡�PHN��Ϊ����ֱ�������Σ���MH=AM=a��Ȼ������PN��AN�ij����ʴ˿ɵõ�tan��PAN=2��tan��PAN= ![]() ��Ȼ���г�����m�ķ�����⼴�ɣ�
��Ȼ���г�����m�ķ�����⼴�ɣ�
�����㾫�����������⣬������Ҫ�˽����ֱ��������(����ֱ��������������ֱ�DZ���ȵ�ֱ�������Σ�����ֱ�������ε�����������ҵ���45��)����Ҫ����������Ǻ����Ķ���(���A�����ҡ����ҡ����С����ж�������A��������Ǻ���)�����֪ʶ���Ǵ���Ĺؼ���


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�D��BC����һ�㣬E��AD���е㣬����A��BC��ƽ���߽�CE���ӳ�����F�� 
��1����֤����AEF�ա�DEC��
��2������BF����AF=DB��AB=AC�����ж��ı���AFBD����״����֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABO�У�AB��OB��OB= ![]() ��AB=1���ѡ�ABO�Ƶ�O��ת150���õ���A1B1O�����A1����Ϊ ��
��AB=1���ѡ�ABO�Ƶ�O��ת150���õ���A1B1O�����A1����Ϊ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���ӳ���Ͷ��һ�����͵��Ӳ�Ʒ��ÿ������ɱ�Ϊ18Ԫ�����������з��֣�ÿ��������y������������۵���x��Ԫ��֮��Ĺ�ϵ���Խ��Ƶؿ���һ�κ���y=��2x+100��������=�ۼ۩�����ɱ���
��1��д��ÿ�µ�����z����Ԫ�������۵���x��Ԫ��֮��ĺ�����ϵʽ��
��2�������۵���Ϊ����Ԫʱ������ÿ���ܻ��350��Ԫ���������۵���Ϊ����Ԫʱ������ÿ���ܻ�����������������Ƕ��٣�
��3��������ز��Ź涨�����ֵ��Ӳ�Ʒ�����۵��۲��ܸ���32Ԫ���������Ҫ���ÿ�²�����350��Ԫ��������ô��������ֲ�Ʒÿ�µ��������ɱ���Ҫ������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ��ֱ������ϵ�У���һRt��ABC����A����1��3����B����3����1����C����3��3������֪��A1AC1���ɡ�ABC��ת�õ��ģ�
��1����д����ת���ĵ������� �� ��ת�����ȣ�
��2���ԣ�1���е���ת����Ϊ���ģ��ֱ���A1AC1˳ʱ����ת90�㡢180��������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Բ�Ľ�Ϊ90�������AOB�У��뾶OA=3��OC=AC��OD= ![]() BD��F�ǻ�AB���е㣮����OCD��CD�۵�����O���ڵ�E������ͼ����Ӱ���ֵ����Ϊ ��
BD��F�ǻ�AB���е㣮����OCD��CD�۵�����O���ڵ�E������ͼ����Ӱ���ֵ����Ϊ �� 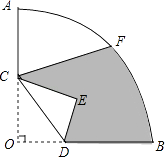
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����Rt��ABC�У���C=90�㣬AC=BC=2����D��E�ֱ��ڱ�AC��AB�ϣ�AD=DE= ![]() AB������DE������ADE�Ƶ�A��ʱ�뷽����ת������ת��Ϊ�ȣ�
AB������DE������ADE�Ƶ�A��ʱ�뷽����ת������ת��Ϊ�ȣ�
��1�����ⷢ��
�ٵ���=0��ʱ�� ![]() =��
=��
�ڵ���=180��ʱ�� ![]() = ��
= ��
��2����չ̽��
���жϣ���0��ܦȣ�360��ʱ�� ![]() �Ĵ�С���ޱ仯�������ͼ2�����θ���֤����
�Ĵ�С���ޱ仯�������ͼ2�����θ���֤����
��3��������
������ת�����У�BE�����ֵΪ��
�ڵ���ADE��ת��B��D��E���㹲��ʱ���߶�CD�ij�Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ABC�У���ABC=90�㣬��ABΪֱ���ġ�O��AC�ڵ�D��E��BC���е㣬����DE��OE�� 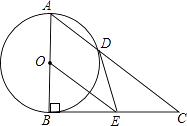
��1����֤��DE���O���У�
��2����֤��BC2=2CDOE��
��3����cosC= ![]() ��DE=4����AD�ij���
��DE=4����AD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������AB��BC��CD��DE��EA��ɵ�ƽ��ͼ�Σ�����1+��2+��3+��4=225�㣬ED��AB�����1�Ķ���Ϊ�� �� 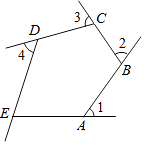
A.55��
B.45��
C.35��
D.25��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com