
【题目】如图所示,一次函数y=kx+b与反比例函数y= ![]() 的图象交于A(2,4),B(﹣4,n)两点.
的图象交于A(2,4),B(﹣4,n)两点. 
(1)分别求出一次函数与反比例函数的表达式;
(2)过点B作BC⊥x轴,垂足为点C,连接AC,求△ACB的面积.
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:初中数学 来源: 题型:
【题目】如图1,已知二次函数y=ax2+bx+c(a、b、c为常数,a≠0)的图象过点O(0,0)和点A(4,0),函数图象最低点M的纵坐标为﹣ ![]() ,直线l的解析式为y=x.
,直线l的解析式为y=x.
(1)求二次函数的解析式;
(2)直线l沿x轴向右平移,得直线l′,l′与线段OA相交于点B,与x轴下方的抛物线相交于点C,过点C作CE⊥x轴于点E,把△BCE沿直线l′折叠,当点E恰好落在抛物线上点E′时(图2),求直线l′的解析式;
(3)在(2)的条件下,l′与y轴交于点N,把△BON绕点O逆时针旋转135°得到△B′ON′,P为l′上的动点,当△PB′N′为等腰三角形时,求符合条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进一批甲、乙两种玩具,已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同.
(1)求每件甲种、乙种玩具的进价分别是多少元?
(2)商场计划购进甲、乙两种玩具共48件,其中甲种玩具的件数少于乙种玩具的件数,商场决定此次进货的总资金不超过1000元,求商场共有几种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F. 
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,正方形ABCD的边长为4,E是边BC上的一点,且BE=1,P是对角线AC上的一动点,连接PB、PE,当点P在AC上运动时,△PBE周长的最小值是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,则下列6个代数式:ab、ac、a+b+c、2a+b、2a﹣b中,其值为正的式子的个数是( ) 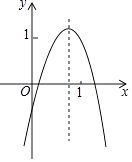
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC内有边长分别为a,b,c的三个正方形,则a,b,c满足的关系式是( ) 
A.b=a+c
B.b=ac
C.b2=a2+c2
D.b=2a=2c
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O(0,0),A(0,1)是正方形OAA1B的两个顶点,以OA1对角线为边作正方形OA1A2B1 , 再以正方形的对角线OA2作正方形OA1A2B1 , …,依此规律,则点A8的坐标是( )
A.(﹣8,0)
B.(0,8)
C.(0,8 ![]() )
)
D.(0,16)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com