练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在直角△ABC中，∠ACB＝90°，∠A＝55°，将其折叠，使点A落在CB上的A′处，折痕CD，则∠A′DB＝ (　　)

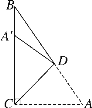
    A. 10° B. 20° C. 30° D. 40°

    【答案】B

    【解析】

    根据Rt△ABC中，∠ACB=90°，∠A=55°，将其折叠，使点A落在边CB上A′处，折痕为CD，可以得到∠B的度数，得到∠A与∠CA′D的关系，从而可以得到∠A′DB的度数．

    ∵Rt△ABC中，∠ACB=90°，∠A=55°，将其折叠，使点A落在边CB上A′处，折痕为CD，
    ∴∠B=90°-∠A=90°-55°=35°，∠A=∠CA′D，
    ∵∠CA′D=∠B+∠A′DB，
    ∴55°=35°+∠A′DB，
    ∴∠A′DB=20°．
    故答案为：20°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】（1）如图（1），已知：在△ABC中，∠BAC＝90°，AB=AC，直线m经过点A，BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.

    （2） 如图（2），将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=,其中为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.

    （3）拓展与应用：如图（3），D、E是D、A、E三点所在直线m上的两动点（D、A、E三点互不重合）,点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形，连接BD、CE,若∠BDA=∠AEC=∠BAC，试判断△DEF的形状.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平行四边形ABCD中，E为CD上一点，连结AE，BD，且AE，BD交于点F，S△DEF∶S△ABF=4∶25，求DE∶EC的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】王华在学习相似三角形时，在北京市义务教育课程改革实验教材第17册书，第31页遇到这样一道题：
    如图1，在△ABC中，P是边AB上的一点，联结CP．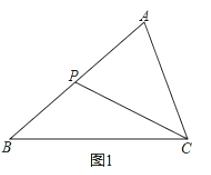

    要使△ACP∽△ABC，还需要补充的一个条件是__，或__．
    （1）王华补充的条件是 ， 或 ．
    （2）请你参考上面的图形和结论，探究、解答下面的问题：
    如图2，在△ABC中，∠A=30°，AC2= AB2+AB．BC．
    求∠C的度数．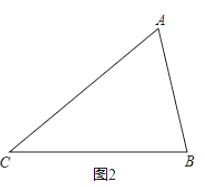

    查看答案和解析>>

    科目：初中数学 来源： 题型：

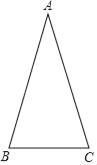
    【题目】如图，在△ABC中，AB=AC，点D在AB边上，点D到点A的距离与点D到点C的距离相等．

    （1）利用尺规作图作出点D，不写作法但保留作图痕迹．

    （2）若△ABC的底边长5，周长为21，求△BCD的周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若正方形的边长为6，则其外接圆半径与内切圆半径的大小分别为（ ）
    A.6，
    B. ，3
    C.6，3
    D. ，

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在四边形ABCD中，对角线AC与BD交于点O，下列各组条件，其中不能判定四边形ABCD是平行四边形的是（　　）

    A. OA＝OC，OB＝ODB. OA＝OC，AB∥CD

    C. AB＝CD，OA＝OCD. ∠ADB＝∠CBD，∠BAD＝∠BCD

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读材料：若m2﹣2mn+2n2﹣8n+16=0，求m、n的值．

    解：∵m2﹣2mn+2n2﹣8n+16=0，∴（m2﹣2mn+n2）+（n2﹣8n+16）=0

    ∴（m﹣n）2+（n﹣4）2=0，∴（m﹣n）2=0，（n﹣4）2=0，∴n=4，m=4．

    根据你的观察，探究下面的问题：

    （1）a2+b2﹣4a+4=0，则a=　　．b=　　．

    （2）已知x2+2y2﹣2xy+6y+9=0，求xy的值．

    （3）已知△ABC的三边长a、b、c都是正整数，且满足2a2+b2﹣4a﹣6b+11=0，求△ABC的周长

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】中秋节来临，小红家自己制作月饼．小红做了三个月饼，1个芝麻馅，2个豆沙馅；小红的爸爸做了两个月饼，1个芝麻馅，1个豆沙馅（除馅料不同，其它都相同）．做好后他们请奶奶品尝月饼，奶奶从小红做的月饼中拿了一个，从小红爸爸做的月饼中拿了一个．请利用列表或画树状图的方法求奶奶拿到的月饼都是豆沙馅的概率．

    查看答案和解析>>

    同步练习册答案