
 若x是在数轴上点A和点B之间的一个整数,请你选择一个合适的数求出你所列代数式的值-1.
若x是在数轴上点A和点B之间的一个整数,请你选择一个合适的数求出你所列代数式的值-1. 分析 由于-2<-$\sqrt{2}$<-1,2$<\sqrt{7}$<3,由此即可确定-$\sqrt{2}$与$\sqrt{7}$取值范围,再即可确定它们之间的整数,即可解答.
解答 解:∵-2<-$\sqrt{2}$<-1,2$<\sqrt{7}$<3,
∴大于-$\sqrt{2}$且小于$\sqrt{7}$的整数为-1、0、1、2,共四个整数,
代数式为:2a+1,
当a=-1时,2a+1=2×(-1)+1=-1.
故答案为:-1.
点评 此题主要考查了无理数的估算能力,由于引进了数轴,我们把数和点对应起来,也就是把“数”和“形”结合起来,二者互相补充,相辅相成,把很多复杂的问题转化为简单的问题,在学习中要注意培养数形结合的数学思想.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a>b>c | B. | c>a>b | C. | c>b>a | D. | a>c>b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
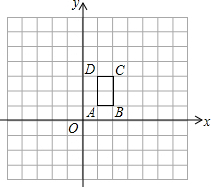 已知:如图,长方形ABCD的顶点坐标分别为A(1,1),B(2,1),C(2,3),D(1,3).
已知:如图,长方形ABCD的顶点坐标分别为A(1,1),B(2,1),C(2,3),D(1,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
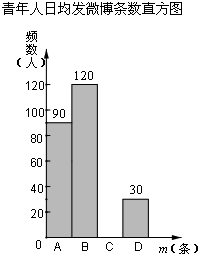 在某项针对18-35岁的青年人每天发微博数量的调查中,设一个人的“日均发微博条数”为m,规定:当0≤m<5时为A级,5≤m<10时为B级,10≤m<15时为C级,15≤m<20时为D级.现随机抽取部分符合年龄条件的青年人开展每人“日均发微博条数”的调查,根据调查数据整理并制作图表如下:
在某项针对18-35岁的青年人每天发微博数量的调查中,设一个人的“日均发微博条数”为m,规定:当0≤m<5时为A级,5≤m<10时为B级,10≤m<15时为C级,15≤m<20时为D级.现随机抽取部分符合年龄条件的青年人开展每人“日均发微博条数”的调查,根据调查数据整理并制作图表如下:| m | 频数 | 百分数 |
| A级(0≤m<5) | 90 | 0.3 |
| B级(5≤m<10) | 120 | a |
| C级(10≤m<15) | b | 0.2 |
| D级(15≤m<20) | 30 | 0.1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com