

分析 (1)由菱形的性质得出MA=MC=$\frac{1}{2}$AC,MB=MD=$\frac{1}{2}$BD,∠BAM=$\frac{1}{2}$∠BAD=30°,∠AMB=90°,得出MB=$\frac{1}{2}$AB=1,由勾股定理求出MA,即可得出对角线AC、BD的长;
(2)连接OB,由等腰三角形的性质得出OA=OD=1,OB⊥AD,由勾股定理求出OB,证出∠OBC=90°,由勾股定理求出OC,即可得出sinα的值;再根据△OCD的面积求出sinβ,即可得出结果;
(3)分两种情况:①当∠APC=90°时,点P是CB与y轴的交点,AP=OB=$\sqrt{3}$,即可得出结果;
②当∠ACP=90°时,求出∠APC=30°,得出AP=2AC=4$\sqrt{3}$,即可得出结果.
解答 解:(1)∵四边形ABCD是菱形,
∴AB=BC=CD=AD=2,MA=MC=$\frac{1}{2}$AC,MB=MD=$\frac{1}{2}$BD,AC⊥BD,
∠BAM=∠DAM=$\frac{1}{2}$∠BAD=30°,AD∥BC,
∴∠AMB=90°,
∴MB=$\frac{1}{2}$AB=1,MA=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
∴AC=2MA=2$\sqrt{3}$,BD=2MB=2;
(2)sinα=2sinβ;理由如下:
连接OB,如图1所示: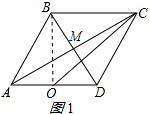
∵点O是边AD的中点,BD=AB=2,
∴OA=OD=1,OB⊥AD,
∴OB=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
∵AD∥BC,
∴OB⊥BC,∠BCO=∠COD=α,
∴∠OBC=90°,
∴OC=$\sqrt{O{B}^{2}+B{C}^{2}}$=$\sqrt{(\sqrt{3})^{2}+{2}^{2}}$=$\sqrt{7}$,
∴sinα=$\frac{OB}{OC}$=$\frac{\sqrt{3}}{\sqrt{7}}$=$\frac{\sqrt{21}}{7}$,
∵△OCD的面积=$\frac{1}{2}$OD•OB=$\frac{1}{2}$OC•CDsinβ,
∴sinβ=$\frac{OD•OB}{OC•CD}$=$\frac{1×\sqrt{3}}{\sqrt{7}×2}$=$\frac{\sqrt{21}}{14}$,
∴sinα=2sinβ;
(3)存在点P,使△PAC为直角三角形,点P坐标为(0,$\sqrt{3}$)或(0,4$\sqrt{3}$);理由如下: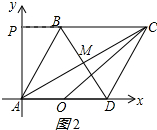
分两种情况:
①当∠APC=90°时,如图2所示:
点P是CB与y轴的交点,
∴AP=OB=$\sqrt{3}$,
∴点P的坐标为(0,$\sqrt{3}$);
②当∠ACP=90°时,如图3所示: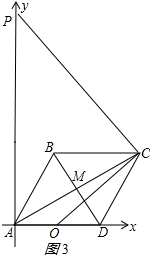
∠PAC=90°-30°=60°,
∴∠APC=30°,
∴AP=2AC=4$\sqrt{3}$,
∴点P的坐标为(0,4$\sqrt{3}$);
综上所述:点P坐标为(0,$\sqrt{3}$)或(0,4$\sqrt{3}$).
点评 本题是四边形综合题目,考查了菱形的性质、勾股定理、含30°角的直角三角形的性质、等腰三角形的性质、三角函数、直角三角形的判定等知识;本题难度较大,综合性强,特别是(3)中,需要进行分类讨论,才能得出结果.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
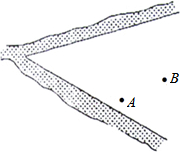 已知A村和B村坐落在两相交公路内(如图所示),为繁荣当地经济,A、B两付计划合建一座物流中心,要求所建物流中心必须满足下列条件:①到两条公路的距离相等;②到A、B两村的距离也相等.
已知A村和B村坐落在两相交公路内(如图所示),为繁荣当地经济,A、B两付计划合建一座物流中心,要求所建物流中心必须满足下列条件:①到两条公路的距离相等;②到A、B两村的距离也相等.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com