
ЁОЬтФПЁПФсВДЖћЗЂЩњСЫРяЪЯ8ЃЎ1МЖЕие№ЃЌФГжабЇзщжЏСЫЯзАЎаФОшПюЛюЖЏЃЌИУаЃНЬбЇаЫШЄаЁзщЖдБОаЃбЇЩњЯзАЎаФОшПюЖюзіСЫвЛДЮЫцЛњГщбљЕїВщЃЌВЂЛцжЦСЫВЛЭъећЕФЦЕЪ§ЗжВМБэКЭЦЕЪ§ЗжВМжБЗНЭМЃЎШчЭМЫљЪОЃК

ЃЈ1ЃЉaЕШгкЖрЩйЃПbЕШгкЖрЩйЃП
ЃЈ2ЃЉВЙШЋЦЕЪ§ЗжВМжБЗНЭМЃЛШєжЦГЩЩШаЮЭГМЦЭМЃЌЧѓОшПюЖюдк![]() жЎМфЕФЩШаЮдВаФНЧЕФЖШЪ§ЃЛ
жЎМфЕФЩШаЮдВаФНЧЕФЖШЪ§ЃЛ
ЃЈ3ЃЉИУаЃЙВга1600УћбЇЩњЃЌЙРМЦетДЮЛюЖЏжаАЎаФОшПюЖюВЛЕЭгк20дЊЕФбЇЩњгаЖрЩйШЫЃП
ЁОД№АИЁПЃЈ1ЃЉ10ЃЌ28%ЃЛЃЈ2ЃЉМћНтЮіЃЌ100.8ЁуЃЛЃЈ3ЃЉ640ШЫ
ЁОНтЮіЁП
ЃЈ1ЃЉЯШРћгУЕквЛзщЕФЦЕЪ§гыЦЕТЪМЦЫуГібљБОШнСПЃЌдйРћгУбљБОШнСПГЫвд20%МДПЩЕУЕНaЕФжЕЃЌгУ14Г§вдбљБОШнСПЕУЕНbЕФжЕЃЛ
ЃЈ2ЃЉЕкЖўзщЕФЦЕЪ§ЮЊ10ЃЌдђПЩВЙШЋЦЕЪ§ЭГМЦЭМЃЌдйгУ360ЁуГЫвдОшПюЖюдк![]() жЎМфЕФШЫЪ§ЕФАйЗжБШМДПЩЃЛ
жЎМфЕФШЫЪ§ЕФАйЗжБШМДПЩЃЛ
ЃЈ3ЃЉИљОнбљБОПЩЕУАЎаФОшПюЖюВЛЕЭгк20дЊЕФАйЗжБШЮЊ28%+12%=40%ЃЌШЛКѓгУзмШЫЪ§ГЫвд40%МДПЩЙРМЦГіАЎаФОшПюЖюВЛЕЭгк20дЊЕФбЇЩњЪ§ЃЎ
НтЃКЃЈ1ЃЉ5ЁТ10%=50ЃЌa=50ЁС20%=10ЃЛb=![]() ЁС100%=28%ЃЛ
ЁС100%=28%ЃЛ
ЃЈ2ЃЉШчЭМЃЌ![]() ЃЌ
ЃЌ
ЃЈ3ЃЉ1600ЁСЃЈ28%+12%ЃЉ=640ЃЈШЫЃЉЃЎ



 МЄЛюЫМЮЌжЧФмбЕСЗПЮЪБЕМбЇСЗЯЕСаД№АИ
МЄЛюЫМЮЌжЧФмбЕСЗПЮЪБЕМбЇСЗЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвдЫФБпаЮ![]() ЕФБп
ЕФБп![]() ЮЊаББпЗжБ№ЯђЭтВрзїЕШбќжБНЧШ§НЧаЮЃЌжБНЧЖЅЕуЗжБ№ЮЊ
ЮЊаББпЗжБ№ЯђЭтВрзїЕШбќжБНЧШ§НЧаЮЃЌжБНЧЖЅЕуЗжБ№ЮЊ![]() ЫГДЮСЌНгетЫФИіЕуЃЌЕУЫФБпаЮ
ЫГДЮСЌНгетЫФИіЕуЃЌЕУЫФБпаЮ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉШчЃЈЭМ1ЃЉЃЎЕБЫФБпаЮ![]() ЮЊе§ЗНаЮЪБЃЌЮвУЧЗЂЯжЫФБпаЮ
ЮЊе§ЗНаЮЪБЃЌЮвУЧЗЂЯжЫФБпаЮ![]() ЪЧе§ЗНаЮЃЛШчЃЈЭМ2ЃЉЃЌЕБЫФБпаЮ
ЪЧе§ЗНаЮЃЛШчЃЈЭМ2ЃЉЃЌЕБЫФБпаЮ![]() ЮЊОиаЮЪБЃЌЧыХаЖЯЃКЫФБпаЮ
ЮЊОиаЮЪБЃЌЧыХаЖЯЃКЫФБпаЮ![]() ЕФаЮзД(ВЛвЊЧѓжЄУї)ЃЛ
ЕФаЮзД(ВЛвЊЧѓжЄУї)ЃЛ
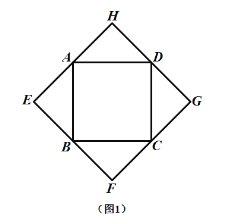
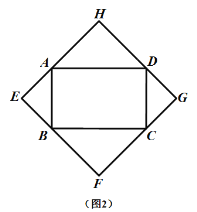
ЃЈ2ЃЉШчЃЈЭМ3ЃЉЃЌЕБЫФБпаЮ![]() ЮЊвЛАуЦНааЫФБпаЮЪБ ЃЌЩш
ЮЊвЛАуЦНааЫФБпаЮЪБ ЃЌЩш![]()
ЂйЪдгУКЌ![]() ЕФДњЪ§ЪНБэЪО
ЕФДњЪ§ЪНБэЪО![]() ЃЛ
ЃЛ
ЂкЧѓжЄЃКЫФБпаЮ![]() ЪЧе§ЗНаЮЃЌ
ЪЧе§ЗНаЮЃЌ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП2018Фъ10дТ23ШеЃЌИлжщАФДѓЧХе§ЪНПЊЭЈЃЌГЩЮЊКсиЈдкСциъбѓЩЯЕФвЛЕРіІРіЕФЗчОА.ДѓЧХжїЬхЙЄГЬЫэЕРЕФЖЋЁЂЮїСНЖЫИїЩшжУСЫвЛИіКЃжаШЫЙЄЕКЃЌРДЯЮНгЧХСККЭКЃЕзЫэЕРЃЌЮїШЫЙЄЕКЩЯЕФAЕуКЭЖЋШЫЙЄЕКЩЯЕФBЕуМфЕФОрРыдМЮЊ5.6ЧЇУзЃЌЕуCЪЧгыЮїШЫЙЄЕКЯрСЌЕФДѓЧХЩЯЕФвЛЕуЃЌAЃЌBЃЌCдквЛЬѕжБЯпЩЯЃЎШчЭМЃЌвЛЫвЙлЙтДЌбигыДѓЧХ![]() ЖЮДЙжБЕФЗНЯђКНааЃЌЕНДяPЕуЪБЙлВтСНИіШЫЙЄЕКЃЌЗжБ№ВтЕУ
ЖЮДЙжБЕФЗНЯђКНааЃЌЕНДяPЕуЪБЙлВтСНИіШЫЙЄЕКЃЌЗжБ№ВтЕУ![]() гыЙлЙтДЌКНЯђ
гыЙлЙтДЌКНЯђ![]() ЕФМаНЧЁЯDPA=18ЁуЃЌЁЯDPB=53ЁуЃЌЧѓДЫЪБЙлЙтДЌЕНДѓЧХACЖЮЕФОрРы
ЕФМаНЧЁЯDPA=18ЁуЃЌЁЯDPB=53ЁуЃЌЧѓДЫЪБЙлЙтДЌЕНДѓЧХACЖЮЕФОрРы![]() ЕФГЄЃЎ
ЕФГЄЃЎ
ВЮПМЪ§ОнЃК![]() Ёу
Ёу![]() ЃЌ
ЃЌ![]() Ёу
Ёу![]() ЃЌ
ЃЌ![]() Ёу
Ёу![]() ЃЌ
ЃЌ![]() Ёу
Ёу![]() ЃЌ
ЃЌ![]() Ёу
Ёу![]() ЃЌ
ЃЌ![]() Ёу
Ёу![]() ЃЎ
ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПбЇаЃЫцЛњГщШЁСЫОХФъМЖВПЗжбЇЩњНјааЬхг§ФЃФтВтЪдЃЌНЋГЩМЈЭГМЦЗжЮіВЂЛцжЦСЫЦЕЪ§ЗжВМБэКЭЭГМЦЭМЃЌАДЕУЗжЛЎЗжГЩAЁЂBЁЂCЁЂDЁЂEЁЂFСљИіЕШМЖЃЌЛцжЦГЩШчЯТЫљЪОЕФСНЗљЭГМЦЭМБэЃЈВЛЭъећЕФЃЉ
ЕШМЖ | ЕУЗжxЃЈЗжЃЉ | ЦЕЪ§ЃЈШЫЃЉ |
A | 95ЃМxЁм100 | 4 |
B | 90ЃМxЁм95 | m |
C | 85ЃМxЁм90 | n |
D | 80ЃМxЁм85 | 24 |
E | 75ЃМxЁм80 | 8 |
F | 70ЃМxЁм75 | 4 |

ЧыФуИљОнЭМБэжаЕФаХЯЂЭъГЩЯТСаЮЪЬтЃК
ЃЈ1ЃЉБОДЮГщбљЕїВщЕФбљБОШнСПЪЧЁЁ ЁЁЃЌЦфжаmЃНЁЁ ЁЁЃЌnЃНЁЁ ЁЁЃЛ
ЃЈ2ЃЉЩШаЮЭГМЦЭМжаEЕШМЖЖдгІЩШаЮЕФдВаФНЧІСЃНЁЁ ЁЁЁуЃЛ
ЃЈ3ЃЉвбжЊИУаЃОХФъМЖЙВга700УћбЇЩњЃЌПЩвдЙРМЦЬхг§ВтЪдГЩМЈдкAЁЂBСНИіЕШМЖЕФШЫЪ§ЙВгаЁЁ ЁЁШЫЃЛ
ЃЈ4ЃЉИУаЃОіЖЈДгБОДЮГщШЁЕФAЕШМЖбЇЩњЃЈМЧЮЊМзЁЂввЁЂБћЁЂЖЁЃЉжаЫцЛњбЁдё2УћзїЮЊДњБэВЮМгШЋЪаЬхг§НЛСїЛюЖЏЃЌЧыФугУСаБэЗЈЛђЛЪїзДЭМЕФЗНЗЈЃЌЧѓЧЁКУГщЕНМзКЭввЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯп![]() ЕФЖЅЕуЮЊЕу
ЕФЖЅЕуЮЊЕу![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓжЄЃКВЛТл![]() ЮЊКЮЪЕЪ§ЃЌИУХзЮяЯпгы
ЮЊКЮЪЕЪ§ЃЌИУХзЮяЯпгы![]() жсзмгаСНИіВЛЭЌЕФНЛЕуЃЛ
жсзмгаСНИіВЛЭЌЕФНЛЕуЃЛ
ЃЈ2ЃЉШєХзЮяЯпЕФЖдГЦжсЮЊжБЯп![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕКЭ
ЕФжЕКЭ![]() ЕузјБъЃЛ
ЕузјБъЃЛ
ЃЈ3ЃЉШчЭМЃЌжБЯп![]() гыЃЈ2ЃЉжаЕФХзЮяЯпВЂгк
гыЃЈ2ЃЉжаЕФХзЮяЯпВЂгк![]() СНЕуЃЌВЂгыЫќЕФЖдГЦжсНЛгкЕу
СНЕуЃЌВЂгыЫќЕФЖдГЦжсНЛгкЕу![]() ЃЌжБЯп
ЃЌжБЯп![]() НЛжБЯп
НЛжБЯп![]() гкЕу
гкЕу![]() ЃЌНЛХзЮяЯпгкЕу
ЃЌНЛХзЮяЯпгкЕу![]() ЃЎЧѓЕБ
ЃЎЧѓЕБ![]() ЮЊКЮжЕЪБЃЌвд
ЮЊКЮжЕЪБЃЌвд![]() ЮЊЖЅЕуЕФЫФБпаЮЮЊЦНааЫФБпаЮЃЎ
ЮЊЖЅЕуЕФЫФБпаЮЮЊЦНааЫФБпаЮЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
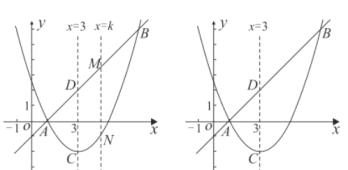
ЁОЬтФПЁПЖўДЮКЏЪ§y=ax2+bx+c(aЁй0)ЕФЭМЯѓШчЭМЃЌШє|ax2+bx+c|=kгаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЌдђkЕФШЁжЕЗЖЮЇЪЧ____ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖдгкЦНУцжБНЧзјБъЯЕxOyжаЕФЕуPКЭЁбMЃЌИјГіШчЯТЖЈвхЃКШєЁбMЩЯДцдкСНИіЕуAЃЌBЃЌЪЙAB=2PMЃЌдђГЦЕуPЮЊЁбMЕФЁАУРКУЕуЁБЃЎ
ЃЈ1ЃЉЕБЁбMАыОЖЮЊ2ЃЌЕуMКЭЕуOжиКЯЪБЃЎ
ЂйЕуP1(Љ2ЃЌ0)ЃЌP2(1ЃЌ1)ЃЌP3(2ЃЌ2)жаЃЌЁбOЕФЁАУРКУЕуЁБЪЧЁЁЁЁЁЁЁЁЃЛ
ЂкШєжБЯпy=2x+bЩЯДцдкЕуPЮЊЁбOЕФЁАУРКУЕуЁБЃЌЧѓbЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉЕуMЮЊжБЯпy=4ЩЯвЛЖЏЕуЃЌвд2ЮЊАыОЖзїЁбMЃЌЕуPЮЊжБЯпy=xЩЯвЛЖЏЕуЃЌЕуPЮЊЁбMЕФЁАУРКУЕуЁБЃЌЧѓЕуMЕФКсзјБъmЕФШЁжЕЗЖЮЇЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
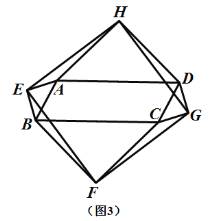
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮABCDжаЃЌЕуGЮЊЖдНЧЯпACЩЯвЛЕуЃЌAG=ABЃЎЁЯCAE=15ЁуЧвAE=ACЃЌСЌНгGEЃЎНЋЯпЖЮAEШЦЕуAФцЪБеыа§зЊЕУЕНЯпЖЮAFЃЌЪЙDF=GEЃЌдђЁЯCAFЕФЖШЪ§ЮЊ________ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкОиаЮABCDжаЃЌAB=8ЃЌAD=6ЃЌPЮЊЩфЯпABЩЯвЛИіЖЏЕуЃЌЙ§PзїPFЁЭACЃЌДЙзуЮЊFЃЌНЛCDгкЕуGЃЌСЌНгCPгыBFНЛгкЕуHЃЌЙ§ЕуCЃЌPЃЌFзїЁбOЃЎ

ЃЈ1ЃЉЕБAP=5ЪБЃЌЧѓжЄЃКЁЯCPB=ЁЯFBCЃЎ
ЃЈ2ЃЉЕБЕуPдкЯпЖЮABЩЯЪБЃЌШєЁїFCHЕФУцЛ§ЕШгкЁїPBHУцЛ§ЕФ4БЖЃЌЧѓDGЕФГЄЃЎ
ЃЈ3ЃЉЕБЁбOгыЁїADCЕФЦфжавЛБпЯрЧаЪБЃЌЧѓЫљгаТњзуЬѕМўЕФAPЕФГЄЃЎ
ЃЈ4ЃЉЕБHНЋЯпЖЮCPЗжГЩ1ЃК4ЕФСНВПЗжЪБЃЌЧѓAPЕФГЄ(жБНгаДГіНсЙћ)ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com