
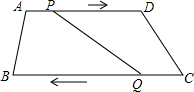
 如图所示,在四边形ABCD中,AD∥BC,AD=24cm,BC=30cm,点P从A向点D以1cm/s的速度运动,到点D即停止.点Q从点C向点B以2cm/s的速度运动,到点B即停止.直线PQ将四边形ABCD截得两个四边形,分别为四边形ABQP和四边形PQCD,则当P,Q两点同时出发,几秒后所截得两个四边形中,其中一个四边形为平行四边形?
如图所示,在四边形ABCD中,AD∥BC,AD=24cm,BC=30cm,点P从A向点D以1cm/s的速度运动,到点D即停止.点Q从点C向点B以2cm/s的速度运动,到点B即停止.直线PQ将四边形ABCD截得两个四边形,分别为四边形ABQP和四边形PQCD,则当P,Q两点同时出发,几秒后所截得两个四边形中,其中一个四边形为平行四边形? 分析 ①若四边形ABQP是平行四边形,则AP=BQ,进而求出t的值;②若四边形PQCD是平行四边形,则PD=CQ,进而求出t的值.
解答 解:设当P,Q两点同时出发,t秒后,四边形ABQP或四边形PQCD是平行四边形,
根据题意可得:
AP=tcm,PD=(24-t)cm,CQ=2tcm,BQ=(30-2t)cm,
①若四边形ABQP是平行四边形,
则AP=BQ,
∴t=30-2t,
解得:t=10,
∴10s后四边形ABQP是平行四边形;
②若四边形PQCD是平行四边形,
则PD=CQ,
∴24-t=2t,
解得:t=8,
∴8s后四边形PQCD是平行四边形;
综上所述:当P,Q两点同时出发,8秒或10秒后,四边形ABQP或四边形PQCD是平行四边形.
点评 此题主要考查了平行四边形的判定,利用分类讨论得出是解题关键.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 甲的成绩稳定 | B. | 乙的成绩较稳定 | ||
| C. | 甲、乙成绩的稳定性相同 | D. | 甲、乙成绩的稳定性无法比较 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB为⊙O的直径,PD切⊙O于点C,与BA的延长线交于点D,DE⊥PO交PO延长线于点E,连接PB,∠EDB=∠EPB.
如图,AB为⊙O的直径,PD切⊙O于点C,与BA的延长线交于点D,DE⊥PO交PO延长线于点E,连接PB,∠EDB=∠EPB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com