
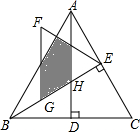
 如图,△ABC是等边三角形,高AD、BE相交于点H,BC=4,在BE上截取BG=2,以GE为边作等边三角形GEF,则△ABH与△GEF重叠(阴影)部分的面积为$\frac{\sqrt{3}}{6}$.
如图,△ABC是等边三角形,高AD、BE相交于点H,BC=4,在BE上截取BG=2,以GE为边作等边三角形GEF,则△ABH与△GEF重叠(阴影)部分的面积为$\frac{\sqrt{3}}{6}$. 分析 根据等边三角形的性质,可得BE的长,∠ABE=∠HBD=30°,根据等边三角形的判定,可得△MEH的形状,根据直角三角形的判定,可得△FPQ的形状,根据面积的和差,可得答案.
解答 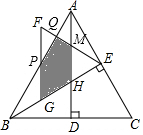 解:∵△ABC是等边三角形,高AD、BE相交于点H,
解:∵△ABC是等边三角形,高AD、BE相交于点H,
∴∠ADB=∠BEC=90°,
∠C=∠ABC=∠BAC=60°,
∠EBC=30°,
BD=EC=$\frac{1}{2}$BC=2,
由勾股定理得:BE=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
在Rt△BDH中,cos30°=$\frac{BD}{BH}$,
BH=$\frac{BD}{cos30°}$=$\frac{2}{\frac{\sqrt{3}}{2}}$=$\frac{4\sqrt{3}}{3}$,
∴EH=BE-BH=2$\sqrt{3}$-$\frac{4\sqrt{3}}{3}$=$\frac{2\sqrt{3}}{3}$,
∵△EFG是等边三角形,
∴FG=EG=2$\sqrt{3}$-2,
∠FEG=∠FGE=∠F=60°,
∵∠MHE=∠BHD=60°,
∴△MEH是等边三角形,
∴S△MEH=$\frac{\sqrt{3}}{4}$×$(\frac{2\sqrt{3}}{3})^{2}$=$\frac{\sqrt{3}}{3}$,
∵∠QEA=180°-90°-60°=30°,
∠BAC=60°,
∴∠FQD=∠AQE=90°
∵∠F=60°,
∴∠FDQ=30°,
△BDG中,∠DBG=30°,∠FGE=60°,
∴∠BDG=30°,
∴BG=DG=2,
∴FD=FG-DG=2$\sqrt{3}$-2-2=2$\sqrt{3}$-4,
Rt△FDQ中,∠FDQ=30°,
∴FQ=$\frac{1}{2}$FD=$\sqrt{3}$-2,
cos30°=$\frac{DQ}{FD}$,
DQ=$\frac{\sqrt{3}}{2}$×$(2\sqrt{3}-4)$=$\sqrt{3}(\sqrt{3}-2)$,
∴S△FDQ=$\frac{1}{2}$FQ•DQ=$\frac{1}{2}$×$(\sqrt{3}-2)×\sqrt{3}(\sqrt{3}-2)$=$\frac{7\sqrt{3}}{2}$-6,
∴S阴影=S△EFG-S△FDQ-S△MEH,
=$\frac{\sqrt{3}}{4}$×$(2\sqrt{3}-2)^{2}$-($\frac{7\sqrt{3}}{2}$-6)-$\frac{\sqrt{3}}{3}$,
=$\frac{\sqrt{3}}{6}$.
故答案为:$\frac{\sqrt{3}}{6}$.
点评 本题考查了等边三角形的判定与性质,利用了等边三角形的判定与性质,直角三角形的判定,利用图形的割补法是求面积的关键.


科目:初中数学 来源: 题型:解答题
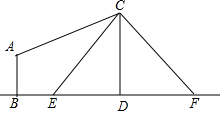 如图,电线杆CD上的C处引拉线CE,CF固定电线杆,在离电线杆6米的B处安置测角仪(点B,E,D在同一直线上),在A处测得电线杆上C处的仰角为30°,已知测角仪的高AB=$\sqrt{3}$米,BE=3米,求拉线CE的长.
如图,电线杆CD上的C处引拉线CE,CF固定电线杆,在离电线杆6米的B处安置测角仪(点B,E,D在同一直线上),在A处测得电线杆上C处的仰角为30°,已知测角仪的高AB=$\sqrt{3}$米,BE=3米,求拉线CE的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
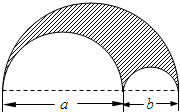 如图,一块直径为a+b的半圆形钢板,从中挖去直径分别为a与b的两个半圆
如图,一块直径为a+b的半圆形钢板,从中挖去直径分别为a与b的两个半圆查看答案和解析>>
科目:初中数学 来源: 题型:解答题
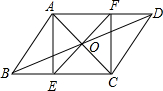 如图,在?ABCD中,AC,BD相交于点O,AE⊥BC,垂足为E,EO的延长线交AD于点F,请你猜想四边形AECF是怎样的四边形?证明你的结论.
如图,在?ABCD中,AC,BD相交于点O,AE⊥BC,垂足为E,EO的延长线交AD于点F,请你猜想四边形AECF是怎样的四边形?证明你的结论.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com