
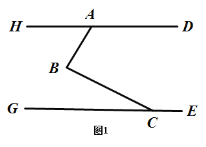
【题目】如图,直线![]() 点
点![]() 在直线
在直线![]() 上,点
上,点![]() 在直线
在直线![]() 上,点
上,点![]() 在直线
在直线![]() 之间,
之间,![]()
![]() .
.
(1)如图1,若![]() ,求
,求![]() 的度数;
的度数;
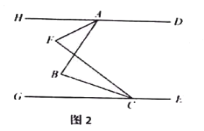
(2)如图2,![]() 平分
平分![]() 平分
平分![]() ,比较
,比较![]() 的大小;
的大小;
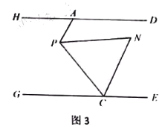
(3)如图3,点![]() 是线段
是线段![]() 上一点,
上一点,![]() 平分
平分![]() 平分
平分![]() ,探究
,探究![]() 和
和![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
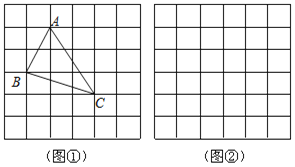
【题目】如图①,在正方形网格中,每个小正方形的边长为1.在网格中构造格点△ABC(即△ABC 三个顶点都在小正方形的顶点处),AB、BC、AC三边的长分别为![]() 、
、![]() 、
、![]() ,利用网格就能计算三角形的面积.
,利用网格就能计算三角形的面积.
(1)请你将△ABC的面积直接填写在横线上.
(2)在图②中画出△DEF,DE、EF、DF三边的长分别为![]() 、
、![]() 、
、![]() .
.
①判断三角形的形状,说明理由.
②求这个三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知顶点为(﹣3,﹣6)的抛物线y=ax2+bx+c经过点(﹣1,﹣4),则下列结论中错误的是( ) 
A.b2>4ac
B.ax2+bx+c≥﹣6
C.若点(﹣2,m),(﹣5,n)在抛物线上,则m>n
D.关于x的一元二次方程ax2+bx+c=﹣4的两根为﹣5和﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,“中国海监50”于上午11时30分在南海海域A处巡逻,观测到岛礁B在北偏东60°,该船以每小时10海里的速度向正东航行到C处,观测岛礁B在北偏东30°,继续向正东航行到D处时,再观测到岛礁B在北偏西30°,当海监船到达C处时恰与岛礁B相距20海里,请你分别确定“中国海监50”从A处到达C处和D处所用的时间.
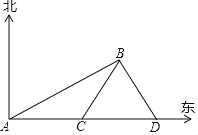
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形OABC和正方形CDEF在平面直角坐标系中,点O,C,F在y轴上,点O为坐标原点,点M为OC的中点,抛物线y=ax2+b经过M,B,E三点,则 ![]() 的值为 .
的值为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个正整数能表示成两个连续偶数的平方差,那么这个正整数为“神秘数”.
如:![]()
![]()
![]()
因此,4,12,20这三个数都是神秘数.
(1)28和2012这两个数是不是神秘数?为什么?
(2)设两个连续偶数为![]() 和
和![]() (其中
(其中![]() 为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由.
为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由.
(3)两个连续奇数的平方差(取正数)是不是神秘数?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家蓝莓采摘园的草莓品质相同,销售价格都是每千克30元,“五一”假期,两家均推出了优惠方案,甲采摘园的优惠方案是:游客进园购买60元的门票,采摘的蓝莓六折优惠;乙采摘园的优惠方案是:游客进园不需购买门票,采摘的蓝莓超过10千克后,超过部分五折优惠,优惠期间,设某游客的蓝莓采摘量为![]() (千克),在甲采摘园所需总费用为
(千克),在甲采摘园所需总费用为![]() (元),在乙采摘园所需总费用为
(元),在乙采摘园所需总费用为![]() (元).
(元).
(1)当采摘量超过10千克时,求![]() 与
与![]() 的关系式;
的关系式;
(2)若要采摘40千克蓝莓,去哪家比较合算?请计算说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,∠BOM=90°,∠DON=90°.
(1)若∠COM=∠AOC,求∠AOD的度数;
(2)若∠COM=![]() ∠BOC,求∠AOC和∠MOD.
∠BOC,求∠AOC和∠MOD.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com