
【题目】垃圾分类是对垃圾传统收集处理方式的改变,是对垃圾进行有效处理的一种科学管理方法.为了增强同学们垃圾分类的意识,某班举行了专题活动,对200件垃圾进行分类整理,得到下列统计图表,请根据统计图表回答问题:(其中A:可回收垃圾;B:厨余垃圾;C:有害垃圾;D:其它垃圾).
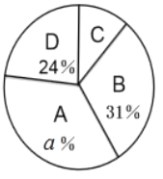
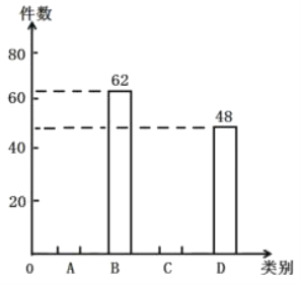
类别 | 件数 |
A | 70 |
B | b |
C | c |
D | 48 |
(1)![]() ________;
________;![]() ________;
________;
(2)补全图中的条形统计图;
(3)有害垃圾C在扇形统计图中所占的圆心角为多少?
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
【题目】某校开展了“创建文明校园”活动周,活动周设置了“A:文明礼仪,B:生态环境,C:交通安全,D:卫生保洁”四个主题,每个学生选一个主题参与.为了解活动开展情况,学校随机抽取了部分学生进行调查,并根据调查结果绘制了如下条形统计图和扇形统计图.
(1)本次随机调查的学生人数是 人;
(2)请你补全条形统计图;
(3)在扇形统计图中,“A”所在扇形的圆心角等于 度;
(4)小明和小华各自随机参加其中的一个主题活动,请用画树状图或列表的方式,求他们恰好同时选中“文明礼仪”或“生态环境”主题的概率.
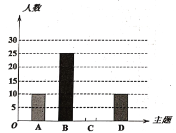
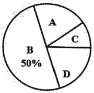
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂制作![]() 两种手工艺品,
两种手工艺品,![]() 每天每件获利比
每天每件获利比![]() 多105元,获利30元的
多105元,获利30元的![]() 与获利240元的
与获利240元的![]() 数量相等.
数量相等.
(1)制作一件![]() 和一件
和一件![]() 分别获利多少元?
分别获利多少元?
(2)工厂安排65人制作![]() ,
,![]() 两种手工艺品,每人每天制作2件
两种手工艺品,每人每天制作2件![]() 或1件
或1件![]() .现在在不增加工人的情况下,增加制作
.现在在不增加工人的情况下,增加制作![]() .已知每人每天可制作1件
.已知每人每天可制作1件![]() (每人每天只能制作一种手工艺品),要求每天制作
(每人每天只能制作一种手工艺品),要求每天制作![]() ,
,![]() 两种手工艺品的数量相等.设每天安排
两种手工艺品的数量相等.设每天安排![]() 人制作
人制作![]() ,
,![]() 人制作
人制作![]() ,写出
,写出![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(3)在(1)(2)的条件下,每天制作![]() 不少于5件.当每天制作5件时,每件获利不变.若每增加1件,则当天平均每件获利减少2元.已知
不少于5件.当每天制作5件时,每件获利不变.若每增加1件,则当天平均每件获利减少2元.已知![]() 每件获利30元,求每天制作三种手工艺品可获得的总利润
每件获利30元,求每天制作三种手工艺品可获得的总利润![]() (元)的最大值及相应
(元)的最大值及相应![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与x轴交于点A,与y轴交点C,抛物线
与x轴交于点A,与y轴交点C,抛物线![]() 过A,C两点,与x轴交于另一点B.
过A,C两点,与x轴交于另一点B.
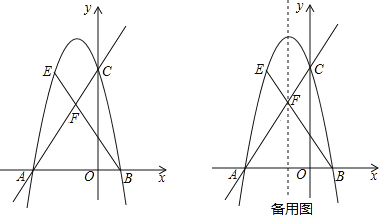
(1)求抛物线的解析式.
(2)在直线AC上方的抛物线上有一动点E,连接BE,与直线AC相交于点F,当![]() 时,求
时,求![]() 的值.
的值.
(3)点N是抛物线对称轴上一点,在(2)的条件下,若点E位于对称轴左侧,在抛物线上是否存在一点M,使以M,N,E,B为顶点的四边形是平行四边形?若存在,直接写出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学六七年级有350名同学去春游,已知2辆A型车和1辆B型车可以载学生100人;1辆A型车和2辆B型车可以载学生110人.
(1)A、B型车每辆可分别载学生多少人?
(2)若租一辆A需要100元,一辆B需120元,请你设计租车方案,使得恰好运送完学生并且租车费用最少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出:如何将一个长为17,宽为1的长方形经过剪一剪,拼一拼,形成一个正方形.(下列所有图中每个小方格的边长都为1,剪拼过程中材料均无剩余)
问题探究:我们从长为5,宽为1的长方形入手.

(1)如图①是一个长为5,宽为1的长方形.把这个长方形剪一剪、拼一拼后形成正方形,则正方形的面积应为_____________,设正方形的边长为![]() ,则
,则![]() _________;
_________;
(2)我们可以把有些带根号的无理数的被开方数表示成两个正整数平方和的形式,比如![]() .类比此,可以将(1)中的
.类比此,可以将(1)中的![]() 表示成
表示成![]() _____________;
_____________;
(3)![]() 的几何意义可以理解为:以长度2和3为直角边的直角三角形的斜边长为
的几何意义可以理解为:以长度2和3为直角边的直角三角形的斜边长为![]() ;类比此,(2)中的
;类比此,(2)中的![]() 可以理解为以长度________和__________为直角边的直角三角形斜边的长;
可以理解为以长度________和__________为直角边的直角三角形斜边的长;
(4)剪一剪:由(3)可画出如图②的分割线,把长方形分成![]() 五部分;
五部分;
(5)拼一拼:把图②中五部分拼接得到如图③的正方形;
问题解决:仿照上面的探究方法请把图④中长为17,宽为1的长方形剪一剪,在图⑤中画出拼成的正方形.(说明:图④的分割过程不作评分要求,只对图⑤中画出的最终结果评分)
![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家规定“中小学生每天在校体育活动时间不低于1小时”.为此,某市就“你每天在校体育活动时间是多少”的问题随机调查了辖区内300名初中学生.根据调查结果绘制成的统计图(部分)如图所示,其中分组情况是:
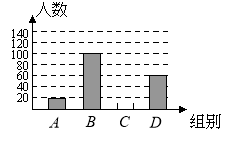
A组:![]() ;B组:
;B组:![]()
C组:![]() D组:
D组:![]()
请根据上述信息解答下列问题:
(1)C组的人数是;
(2)本次调查数据的中位数落在组内;
(3)若该辖区约有24 000名初中学生,请你估计其中达国家规定体育活动时间的人约有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 的图象与x轴负半轴交于点A(-1,0),与y轴正半轴交与点B,顶点为P,且OB=3OA,一次函数y=kx+b的图象经过A、B.
的图象与x轴负半轴交于点A(-1,0),与y轴正半轴交与点B,顶点为P,且OB=3OA,一次函数y=kx+b的图象经过A、B.

(1) 求一次函数解析式;
(2)求顶点P的坐标;
(3)平移直线AB使其过点P,如果点M在平移后的直线上,且![]() ,求点M坐标;
,求点M坐标;
(4)设抛物线的对称轴交x轴与点E,联结AP交y轴与点D,若点Q、N分别为两线段PE、PD上的动点,联结QD、QN,请直接写出QD+QN的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某青春党支部在精准扶贫活动中,给结对帮扶的贫困家庭赠送甲、乙两种树苗让其栽种.已知乙种树苗的价格比甲种树苗贵10元,用480元购买乙种树苗的棵数恰好与用360元购买甲种树苗的棵数相同.
(1)求甲、乙两种树苗每棵的价格各是多少元?
(2)在实际帮扶中,他们决定再次购买甲、乙两种树苗共50棵,此时,甲种树苗的售价比第一次购买时降低了10%,乙种树苗的售价不变,如果再次购买两种树苗的总费用不超过1500元,那么他们最多可购买多少棵乙种树苗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com