
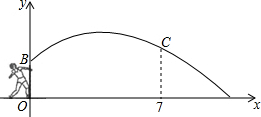
 如图是医学生投掷铅球时,铅球运行的高度y(m)与水平距离x(m)的函数图象,其解析式为y=-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{3}{5}$.
如图是医学生投掷铅球时,铅球运行的高度y(m)与水平距离x(m)的函数图象,其解析式为y=-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{3}{5}$.分析 (1)令y=0,即0=-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{3}{5}$,解方程即可.在实际问题中,注意负值舍去;
(2)把x=7代入y=-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{3}{5}$,求出y的值即为此时铅球距离地面的高度.
解答 解:(1)由题意可知,把y=0代入解析式得:
0=-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{3}{5}$,
解方程得x1=10,x2=-2(舍去),
∴这名学生铅球推出的水平距离是10米;
(2)把x=7代入y=-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{3}{5}$,得:y=-$\frac{1}{12}$×72+$\frac{2}{3}$×7+$\frac{3}{5}$=$\frac{71}{60}$,
∴此时铅球距离地面的高度是$\frac{71}{60}$米.
点评 本题主要考查了二次函数的实际应用,楚铅球落地时,即y=0,测量运动员成绩,也就是求x的值以及知道铅球在空中飞行的水平距离7米,即x=7时,求y的值,此题为数学建模题,借助二次函数解决实际问题.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:初中数学 来源: 题型:解答题
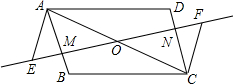 如图,O为?ABCD的对角线AC的中点,过点O的一条直线分别与AB、CD交于点M、N,点E、F在直线MN上,且OE=OF.
如图,O为?ABCD的对角线AC的中点,过点O的一条直线分别与AB、CD交于点M、N,点E、F在直线MN上,且OE=OF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
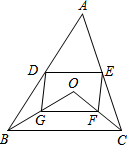 如图,D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点.O是△ABC内的动点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.
如图,D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点.O是△ABC内的动点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
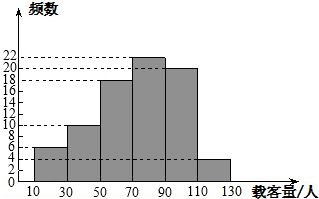 为了解我市3路公共汽车的运营情况,公交部门随机统计了某天3路公共汽车每个运行班次的载客量,得到如下频数分布直方图.如果以各组的组中值代表各组实际数据,请分析统计数据完成下列问题.(注:一个小组的组中值是指这个小组的两个端点数的平均数)
为了解我市3路公共汽车的运营情况,公交部门随机统计了某天3路公共汽车每个运行班次的载客量,得到如下频数分布直方图.如果以各组的组中值代表各组实际数据,请分析统计数据完成下列问题.(注:一个小组的组中值是指这个小组的两个端点数的平均数)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com