
分析 证明△FPP∽△EAQ,则∠PFH=∠EAH,然后根据CDFA四点共圆,得到∠PFH=∠EAH,从而证明△AEM是等腰三角形,然后证明△MHE是等腰三角形即可证得.
解答 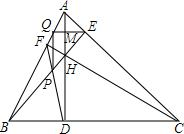 证明:∵AFHE共圆,
证明:∵AFHE共圆,
∴△BHF∽△BAE
∴$\frac{BH}{BA}=\frac{FH}{EA}$,
又∵PQ‖AH,
∴$\frac{BH}{BA}=\frac{PH}{QA}$,
∴$\frac{PH}{QA}=\frac{FH}{EA}$,
又∵∠FHP=∠EAQ,
∴△FHP∽EAQ,
∴∠PFH=∠AEQ.
∵∠ADC=∠AFC=90°,
∴CDFA共圆,
∴∠PFH=∠EAH,
∴∠EAH=∠AEQ,
∴AM=EM,
又∵∠AEH=90°,
∴∠EAH+∠AHE=90°,AEM+∠MEH=90°,
∴∠MEH=∠AHE,
∴MH=ME,
∴AM=MH,即直线QE平分线段AH.
点评 本题考查了三角形的相似以及等腰三角形的判定,证明∠HAE=∠AFQ,得到△AEM是等腰三角形是关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
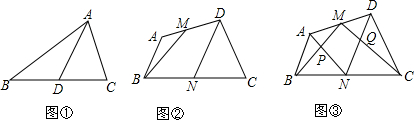
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
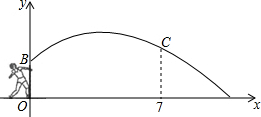 如图是医学生投掷铅球时,铅球运行的高度y(m)与水平距离x(m)的函数图象,其解析式为y=-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{3}{5}$.
如图是医学生投掷铅球时,铅球运行的高度y(m)与水平距离x(m)的函数图象,其解析式为y=-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{3}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
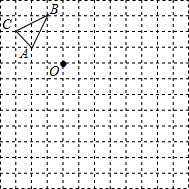 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)和格点O.
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)和格点O.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com