
分析 (1)直接利用概率公式计算即可求出摸出的球是红球和黄球的概率;
(2)设放入红球x个,则黄球为(7-x)个,由摸出两种球的概率相同建立方程,解方程即可求出7个球中红球和黄球的数量分别是多少.
解答 解:(1)∵袋子中装有3个红球和6个黄球,
∴随机摸出一球是红球和黄球的概率分别是$\frac{3}{6+3}$=$\frac{1}{3}$,$\frac{6}{6+3}$=$\frac{2}{3}$;
(2)设放入红球x个,则黄球为(7-x)个,由题意列方程得:
$\frac{3+x}{9+7}=\frac{6+7-x}{9+7}$,
解得:x=5.
所以这7个球中红球和黄球的数量分别应是5个和2个.
点评 本题考查的是求随机事件的概率,解决这类题目要注意具体情况具体对待.用到的知识点为:可能性等于所求情况数与总情况数之比.


科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x=6}\\{y=4}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=4}\\{y=8}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=4}\\{y=6}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=9}\\{y=-1}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 平均数 | B. | 中位数 | C. | 极差 | D. | 众数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
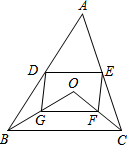 如图,D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点.O是△ABC内的动点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.
如图,D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点.O是△ABC内的动点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC的面积为1.第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,要使得到的三角形的面积超过2015,最少经过( )次操作.
如图,△ABC的面积为1.第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,要使得到的三角形的面积超过2015,最少经过( )次操作.| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com