
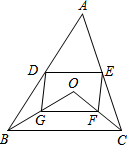
 如图,D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点.O是△ABC内的动点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.
如图,D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点.O是△ABC内的动点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.分析 (1)首先利用三角形中位线的性质得出DE∥BC,DE=$\frac{1}{2}$BC,同理,GF∥BC,GF=$\frac{1}{2}$BC,即可得出DE∥GF,DE=GF即可得出四边形DGFE是平行四边形;
(2)OA=BC时四边形DGFE是菱形,利用(1)中所求,只要邻边再相等即可得出答案.
解答 (1)证明:∵D、E分别是边AB、AC的中点.
∴DE∥BC,DE=$\frac{1}{2}$BC.
同理,GF∥BC,GF=$\frac{1}{2}$BC.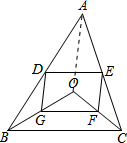
∴DE∥GF,DE=GF.
∴四边形DEFG是平行四边形;
(2)OA=BC时四边形DGFE是菱形,
理由如下:
连接OA.由(1)得出四边形DEFG是平行四边形,
∴AO=BC,
∴GD=$\frac{1}{2}$AO,GF=$\frac{1}{2}$BC,
∴DG=GE,
∴平行四边形DEFG是菱形.
点评 本题考查了三角形的中位线平行于第三边并且等于第三边的一半,平行四边形的判定,菱形的判定以及平行四边形与菱形的关系,熟记的定理和性质是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
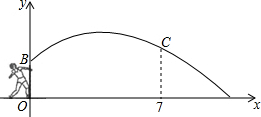 如图是医学生投掷铅球时,铅球运行的高度y(m)与水平距离x(m)的函数图象,其解析式为y=-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{3}{5}$.
如图是医学生投掷铅球时,铅球运行的高度y(m)与水平距离x(m)的函数图象,其解析式为y=-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{3}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | 1 | D. | -$\frac{3}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com