
分析 (1)首先求出两个数的立方的值是多少,然后比较出每组两个数的立方的大小关系,即可判断出原来两个数的大小关系.
(2)首先求出两个数的平方的值是多少,然后比较出每组两个数的平方的大小关系,即可判断出原来两个数的大小关系.
解答 解:(1)23=8,${(\root{3}{9})}^{3}$=9,
∵8<9,
∴2<$\root{3}{9}$.
(2)${(3\sqrt{2})}^{2}$=18,${(2\sqrt{3})}^{2}$=12,
∵18>12,
∴3$\sqrt{2}$>2$\sqrt{3}$.
故答案为:<、>.
点评 此题主要考查了实数大小比较的方法,要熟练掌握,解答此题的关键是比较出每组两个数的立方或平方的大小关系.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:解答题
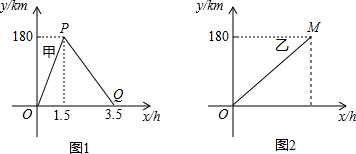
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 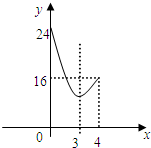 | B. | 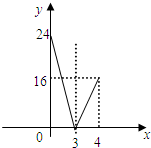 | ||
| C. | 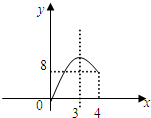 | D. | 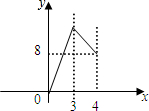 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x=6}\\{y=4}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=4}\\{y=8}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=4}\\{y=6}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=9}\\{y=-1}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
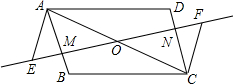 如图,O为?ABCD的对角线AC的中点,过点O的一条直线分别与AB、CD交于点M、N,点E、F在直线MN上,且OE=OF.
如图,O为?ABCD的对角线AC的中点,过点O的一条直线分别与AB、CD交于点M、N,点E、F在直线MN上,且OE=OF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
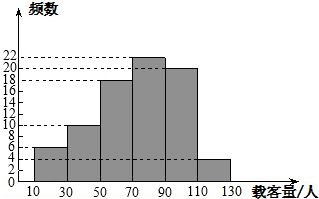 为了解我市3路公共汽车的运营情况,公交部门随机统计了某天3路公共汽车每个运行班次的载客量,得到如下频数分布直方图.如果以各组的组中值代表各组实际数据,请分析统计数据完成下列问题.(注:一个小组的组中值是指这个小组的两个端点数的平均数)
为了解我市3路公共汽车的运营情况,公交部门随机统计了某天3路公共汽车每个运行班次的载客量,得到如下频数分布直方图.如果以各组的组中值代表各组实际数据,请分析统计数据完成下列问题.(注:一个小组的组中值是指这个小组的两个端点数的平均数)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com