
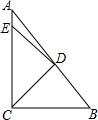
 如图,在Rt△ABC中,∠ACB=90°,点E在AC边上,且与点B关于CD对称,若∠A=40°,则∠ADE=10°.
如图,在Rt△ABC中,∠ACB=90°,点E在AC边上,且与点B关于CD对称,若∠A=40°,则∠ADE=10°.  名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:解答题
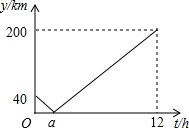 甲、乙两车要从M地沿同一条公路运输一批物资到N地,乙车比甲车先行驶1h,设甲车与乙车之间的距离为y(单位:km),甲车行驶时间为t(单位:h),y与t之间的函数关系如图所示(假设甲、乙两车速度始终保持不变).结合图象解答下列问题:
甲、乙两车要从M地沿同一条公路运输一批物资到N地,乙车比甲车先行驶1h,设甲车与乙车之间的距离为y(单位:km),甲车行驶时间为t(单位:h),y与t之间的函数关系如图所示(假设甲、乙两车速度始终保持不变).结合图象解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解旬河水中汞含量是否符合规定标准 | |
| B. | 了解县师训教研中心36名员工的健康状况 | |
| C. | 商家为了解某一批“电子白板”的使用寿命 | |
| D. | 为了解空气中PM2.5含量 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
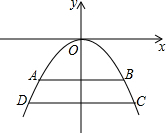 某拱桥的截面呈抛物线形,以抛物线的顶点为原点,以抛物线的对称轴为y轴建立平面直角坐标系(如图所示),抛物线的解析式为y=-$\frac{1}{2}$x2,水面AB到拱顶O的距离为2米.
某拱桥的截面呈抛物线形,以抛物线的顶点为原点,以抛物线的对称轴为y轴建立平面直角坐标系(如图所示),抛物线的解析式为y=-$\frac{1}{2}$x2,水面AB到拱顶O的距离为2米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
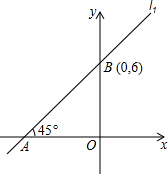 如图,平面直角坐标系中画出了函数l1:y1=kx+b的图象.
如图,平面直角坐标系中画出了函数l1:y1=kx+b的图象.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com