
【题目】定义一种对正整数n的“C运算”:①当n为奇数时,结果为3n+1;②当n为偶数时,结果为![]() (其中k是使
(其中k是使![]() 为奇数的正整数)并且运算重复进行,例如,n=66时,其“C运算”如下:
为奇数的正整数)并且运算重复进行,例如,n=66时,其“C运算”如下:
![]()
若n=26,则第2019次“C运算”的结果是_____.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
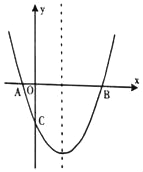
【题目】如图,抛物线y=ax2+bx﹣![]() 经过A(﹣1,0),B(5,0)两点.
经过A(﹣1,0),B(5,0)两点.
(1)求此抛物线的解析式;
(2)在抛物线的对称轴上有一点P,使得PA+PC的值最小时,求△ABP的面积;
(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,直接写出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以直线![]() 上一点
上一点![]() 为端点作射线
为端点作射线![]() ,使
,使![]() ,将一块直角三角板的直角顶点放在
,将一块直角三角板的直角顶点放在![]() 处,一边
处,一边![]() 放在射线
放在射线![]() 上,将直角三角板
上,将直角三角板![]() 绕点
绕点![]() 逆时针方向旋转直至
逆时针方向旋转直至![]() 边第一次重合在射线
边第一次重合在射线![]() 上停止.
上停止.
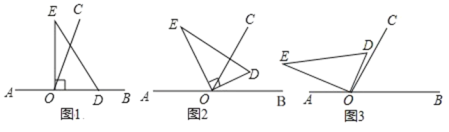
(1)如图1,边![]() 在射线
在射线![]() 上,则
上,则![]() ;
;
(2)如图2,若![]() 恰好平分
恰好平分![]() ,则
,则![]() ;
;
(3)如图3,若![]() ,则
,则![]() ;
;
(4)在旋转过程中,![]() 与
与![]() 始终保持的数量关系是 ,并请说明理由.
始终保持的数量关系是 ,并请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题:①全等三角形的对应边上的中线,高线,对应角的平分线对应相等;②两边和其中一边上的中线(或第三边上的中线)对应相等的两个三角形全等;③两角和其中一角的角平分线(或第三角的角平分线)对应相等的两个三角形全等;④两边和其中一边上的高线(或第三边上的高线)对应相等的两个三角形全等.其中正确命题有________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图,则一次函数y=bx+b2﹣4ac与反比例函数y=![]() 在同一坐标系内的图象大致为( )
在同一坐标系内的图象大致为( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线L1:y=ax2+bx+c(a,b,c是常数,abc≠0)与直线L2都经过y轴上的一点P,且抛物线L1与顶点Q在直线L2上,则称此直线L2与该抛物线L1具有“一带一路”关系,此时,直线L2叫做抛物线L1的“带线”,抛物线L1叫做直L2的“路线”.
(1) 若直线y=mx+1与抛物线y=x2-2x+n具有“一带一路”关系,则m+n=_______.
(2) 若某“路线”L1的顶点在反比例函数![]() 的图像上,它的“带线” L2的解析式为y=2x-4,则此“路线”L的解析式为:_____________.
的图像上,它的“带线” L2的解析式为y=2x-4,则此“路线”L的解析式为:_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
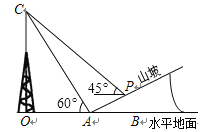
【题目】如图所示,某人在山坡坡脚A处测得电视塔尖点C 的仰角为60°,沿山坡向上走到P处再测得C的仰角为45°,已知OA=200米,山坡坡度为![]() (即tan∠PAB=
(即tan∠PAB=![]() ),且O、A、B在同一条直线上,求电视塔OC的高度以及此人所在位置点P的垂直高度.(测倾器的高度忽略不计,结果保留根号)
),且O、A、B在同一条直线上,求电视塔OC的高度以及此人所在位置点P的垂直高度.(测倾器的高度忽略不计,结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
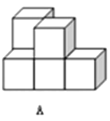
【题目】在桌面上,有若干个完全相同的小正方体堆成的一个几何体![]() ,如图所示.
,如图所示.
(1)请画出这个几何体![]() 的三视图.
的三视图.
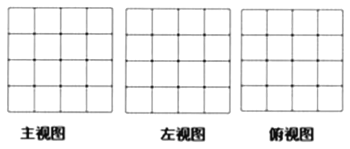
(2)若将此几何体![]() 的表面喷上红漆(放在桌面上的一面不喷),则三个面上是红色的小正方体有 个.
的表面喷上红漆(放在桌面上的一面不喷),则三个面上是红色的小正方体有 个.
(3)若现在你的手头还有一些相同的小正方体可添放在几何体![]() 上,要保持主视图和左视图不变,则最多可以添加___个小正方体.
上,要保持主视图和左视图不变,则最多可以添加___个小正方体.
(4)若另一个几何体![]() 与几何体
与几何体![]() 的主视图和左视图相同,而小正方体个数则比几何体
的主视图和左视图相同,而小正方体个数则比几何体![]() 多1个,请在图2中画出几何体
多1个,请在图2中画出几何体![]() 的俯视图中的任意两种.
的俯视图中的任意两种.
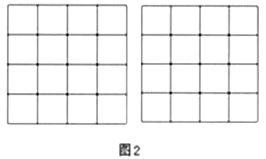
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节放假期间,某学校计划租用![]() 辆客车送
辆客车送![]() 名师生参加研学活动,现有甲、乙两种客车,它们的载客量和租金如下表,设租用甲种客车
名师生参加研学活动,现有甲、乙两种客车,它们的载客量和租金如下表,设租用甲种客车![]() 辆,租车总费用为
辆,租车总费用为![]() 元.
元.
甲种客车 | 乙种客车 | |
载客量(人/辆) |
|
|
租金(元/辆) |
|
|
(1)求出![]() (元)与
(元)与![]() (辆)之间函数关系式;
(辆)之间函数关系式;
(2)求出自变量的取值范围;
(3)选择怎样的租车方案所需的费用最低?最低费用多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com