
【题目】如图所示,某人在山坡坡脚A处测得电视塔尖点C 的仰角为60°,沿山坡向上走到P处再测得C的仰角为45°,已知OA=200米,山坡坡度为![]() (即tan∠PAB=
(即tan∠PAB=![]() ),且O、A、B在同一条直线上,求电视塔OC的高度以及此人所在位置点P的垂直高度.(测倾器的高度忽略不计,结果保留根号)
),且O、A、B在同一条直线上,求电视塔OC的高度以及此人所在位置点P的垂直高度.(测倾器的高度忽略不计,结果保留根号)
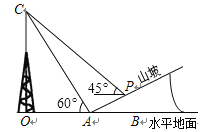
【答案】(50![]() -50)米.
-50)米.
【解析】试题分析:在直角△AOC中,利用三角函数即可求解;在图中共有三个直角三角形,即Rt△AOC、Rt△PCF、Rt△PAE,利用60°、45°以及坡度比,分别求出CO、CF、PE,然后根据三者之间的关系,列方程求解即可解决.
试题解析:过点P作PE⊥OB于点E,PF⊥CO于点F,
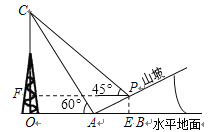
在Rt△AOC中,AO=200米,∠CAO=60°,
∴CO=AOtan60°=200![]() (米)
(米)
(2)设PE=x米,
∵tan∠PAB=![]() ,
,
∴AE=3x.
在Rt△PCF中,
∠CPF=45°,CF=200![]() -x,PF=OA+AE=200+3x,
-x,PF=OA+AE=200+3x,
∵PF=CF,
∴200+3x=200![]() -x,
-x,
解得x=50(![]() -1)米.
-1)米.
答:电视塔OC的高度是200![]() 米,所在位置点P的铅直高度是50(
米,所在位置点P的铅直高度是50(![]() -1)米.
-1)米.


 灵星计算小达人系列答案
灵星计算小达人系列答案科目:初中数学 来源: 题型:
【题目】定义一种对正整数n的“C运算”:①当n为奇数时,结果为3n+1;②当n为偶数时,结果为![]() (其中k是使
(其中k是使![]() 为奇数的正整数)并且运算重复进行,例如,n=66时,其“C运算”如下:
为奇数的正整数)并且运算重复进行,例如,n=66时,其“C运算”如下:
![]()
若n=26,则第2019次“C运算”的结果是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
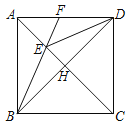
【题目】已知:如图,边长为1的正方形ABCD中,AC 、DB交于点H.DE平分∠ADB,交AC于点E.联结BE并延长,交边AD于点F.
(1)求证:DC=EC;
(2)求△EAF的面积.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
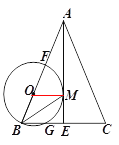
【题目】如图,在△ABC中,AB=AC,AE是BC边上的高线,BM平分∠ABC交AE于点M,经过B,M 两点的⊙O交BC于点G,交AB于点F ,FB为⊙O的直径.
(1)求证:AM是⊙O的切线
(2)当BE=3,cosC=![]() 时,求⊙O的半径.
时,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线![]() 与
与![]() 轴、
轴、![]() 轴分別交于
轴分別交于![]() 、
、![]() 两点,
两点,![]() 是
是![]() 的中点,
的中点,![]() 是线段
是线段![]() 上一点.
上一点.
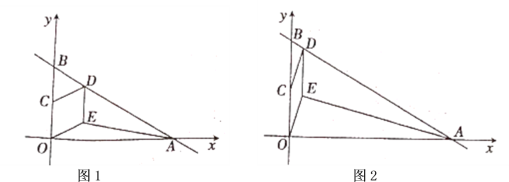
(1)求点![]() 、
、![]() 的坐标;
的坐标;
(2)若四边形![]() 是菱形,如图1,求
是菱形,如图1,求![]() 的面积;
的面积;
(3)若四边形![]() 是平行四边形,如图2,设点
是平行四边形,如图2,设点![]() 的横坐标为
的横坐标为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数关系式.
的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强学生的身体素质,教育行政部门规定学生每天户外活动的平均时间不少于![]() 小时,小明为了解本班学生参加户外活动的情况,特进行了问卷调查.
小时,小明为了解本班学生参加户外活动的情况,特进行了问卷调查.
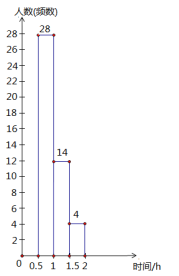
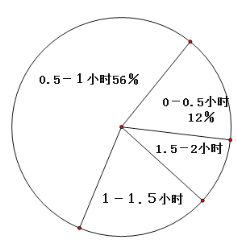
(1)在进行问卷调查时有如下步骤,按顺序排列为________(填序号).
①发问卷,让被调查人填写;②设计问卷;③对问卷的数据进行收集与整理;
④收回问卷;⑤得出结论.
(2)小明根据调查结果,就本班学生每天参加户外活动的平均时间绘制了以下两幅不完整的统计图(图中![]() 表示大于等于
表示大于等于![]() 同时小于
同时小于![]() ,图中类似的记号均表示这一含义),请你根据图中提供的信息解答下列问题:
,图中类似的记号均表示这一含义),请你根据图中提供的信息解答下列问题:
①在这次调查中共调查了多少名学生?
②通过计算补全频数分布直方图;
③请你根据以上统计结果,就学生参加户外活动情况提出建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点![]() 在数轴上所对应的数分别是
在数轴上所对应的数分别是![]() ,其中
,其中![]() 满足
满足![]() .
.
(1)求![]() 的值;
的值;
(2)数轴上有一点![]() ,使得
,使得![]() ,求点
,求点![]() 所对应的数;
所对应的数;
(3)点![]() 为
为![]() 中点,
中点,![]() 为原点,数轴上有一动点
为原点,数轴上有一动点![]() ,求
,求![]() 的最小值及点
的最小值及点![]() 所对应的数的取值范围.
所对应的数的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com