练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知m是6的相反数，n比m的相反数小2，则m-n等于( )

    A. 4 B. 8 C. -2 D. -10

    【答案】D

    【解析】

    由题意可得m=-6，n=6-2=4，代入即可求解．

    由题意可得m=-6，n=6-2=4，
    则m-n=-6-4=-10．
    故选D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】一元二次方程x2-8x-1=0配方后可变形为（ ）．

    A．（x+4）2=17 B．（x+4）2=15 C．（x-4）2=17 D．（x-4）2=15

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】由四舍五入得到的近似数37.6，精确到_____位，它表示大于或等于_____，而小于_____ 的数

    查看答案和解析>>

    科目：初中数学 来源： 题型：

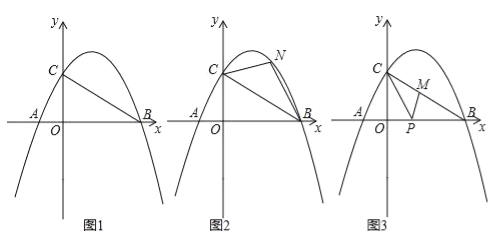
    【题目】如图1，抛物线y=﹣ [（x﹣2）2+n]与x轴交于点A（m﹣2，0）和B（2m+3，0）（点A在点B的左侧），与y轴交于点C，连结BC．

    （1）求m、n的值；

    （2）如图2，点N为抛物线上的一动点，且位于直线BC上方，连接CN、BN．求△NBC面积的最大值；

    （3）如图3，点M、P分别为线段BC和线段OB上的动点，连接PM、PC，是否存在这样的点P，使△PCM为等腰三角形，△PMB为直角三角形同时成立？若存在，求出点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】分解因式：a2﹣b2=

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，BE⊥CD，BE＝DE，BC＝DA．

    求证：（1）△BEC≌△DAE；

    （2）DF⊥BC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】PM2.5是指大气中直径小于或等于2.5微米的颗粒物，2.5微米等于0.000 0025米，把0.000 0025用科学记数法表示为（ ）
    A.2.5×106
    B.0.25×10﹣5
    C.25×10﹣7
    D.2.5×10﹣6

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读理解：

    我们把满足某种条件的所有点所组成的图形，叫做符合这个条件的点的轨迹．

    例如：角的平分线是到角的两边距离相等的点的轨迹．

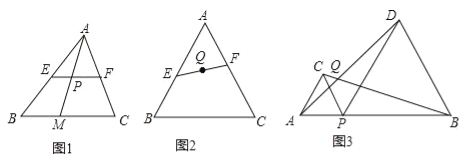
    问题：如图1，已知EF为△ABC的中位线，M是边BC上一动点，连接AM交EF于点P，那么动点P为线段AM中点．

    理由：∵线段EF为△ABC的中位线，∴EF∥BC，

    由平行线分线段成比例得：动点P为线段AM中点．

    由此你得到动点P的运动轨迹是： ．

    知识应用：

    如图2，已知EF为等边△ABC边AB、AC上的动点，连结EF；若AF=BE，且等边△ABC的边长为8，求线段EF中点Q的运动轨迹的长．

    拓展提高：

    如图3，P为线段AB上一动点（点P不与点A、B重合），在线段AB的同侧分别作等边△APC和等边△PBD，连结AD、BC，交点为Q．

    （1）求∠AQB的度数；

    （2）若AB=6，求动点Q运动轨迹的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某同学做了四道题：①3m+4n=7mn；②（﹣2a2）3=﹣8a6；③6x6÷2x2=3x3；④y3xy2=xy5 ， 其中正确的题号是（ ）
    A.②④
    B.①③
    C.①②
    D.③④

    查看答案和解析>>

    同步练习册答案