
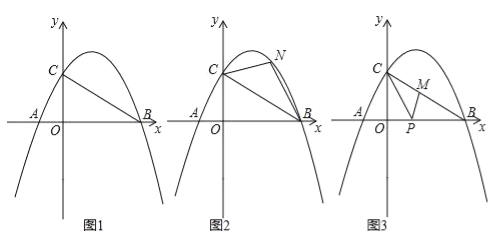
【题目】如图1,抛物线y=﹣![]() [(x﹣2)2+n]与x轴交于点A(m﹣2,0)和B(2m+3,0)(点A在点B的左侧),与y轴交于点C,连结BC.
[(x﹣2)2+n]与x轴交于点A(m﹣2,0)和B(2m+3,0)(点A在点B的左侧),与y轴交于点C,连结BC.
(1)求m、n的值;
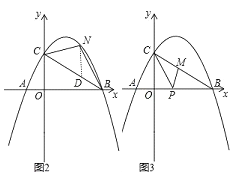
(2)如图2,点N为抛物线上的一动点,且位于直线BC上方,连接CN、BN.求△NBC面积的最大值;
(3)如图3,点M、P分别为线段BC和线段OB上的动点,连接PM、PC,是否存在这样的点P,使△PCM为等腰三角形,△PMB为直角三角形同时成立?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】(1)m=1,n=﹣9;(2)![]() ;(3)存在,P点坐标为(
;(3)存在,P点坐标为(![]() ,0)或(
,0)或(![]() ,0).
,0).
【解析】
试题分析:(1)利用抛物线的解析式确定对称轴为直线x=2,再利用对称性得到2﹣(m﹣2)=2m+3﹣2,解方程可得m的值,从而得到A(﹣1,0),B(5,0),然后把A点坐标代入y=﹣![]() [(x﹣2)2+n]可求出n的值;(2)作ND∥y轴交BC于D,如图2,利用抛物线解析式确定C(0,3),再利用待定系数法求出直线BC的解析式为y=﹣
[(x﹣2)2+n]可求出n的值;(2)作ND∥y轴交BC于D,如图2,利用抛物线解析式确定C(0,3),再利用待定系数法求出直线BC的解析式为y=﹣![]() x+3,设N(x,﹣
x+3,设N(x,﹣![]() x2+
x2+![]() x+3),则D(x,﹣
x+3),则D(x,﹣![]() x+3),根据三角形面积公式,利用S△NBC=S△NDC+S△NDB可得S△BCN=﹣
x+3),根据三角形面积公式,利用S△NBC=S△NDC+S△NDB可得S△BCN=﹣![]() x2+
x2+![]() x,然后利用二次函数的性质求解;(3)先利用勾股定理计算出BC=
x,然后利用二次函数的性质求解;(3)先利用勾股定理计算出BC=![]() ,再分类讨论:当∠PMB=90°,则∠PMC=90°,△PMC为等腰直角三角形,MP=MC,设PM=t,则CM=t,MB=
,再分类讨论:当∠PMB=90°,则∠PMC=90°,△PMC为等腰直角三角形,MP=MC,设PM=t,则CM=t,MB=![]() ﹣t,证明△BMP∽△BOC,利用相似比可求出BP的长,再计算OP后可得到P点坐标;当∠MPB=90°,则MP=MC,设PM=t,则CM=t,MB=
﹣t,证明△BMP∽△BOC,利用相似比可求出BP的长,再计算OP后可得到P点坐标;当∠MPB=90°,则MP=MC,设PM=t,则CM=t,MB=![]() ﹣t,证明△BMP∽△BCO,利用相似比可求出BP的长,再计算OP后可得到P点坐标.
﹣t,证明△BMP∽△BCO,利用相似比可求出BP的长,再计算OP后可得到P点坐标.
试题解析:(1)∵抛物线的解析式为y=﹣![]() [(x﹣2)2+n]=﹣
[(x﹣2)2+n]=﹣![]() (x﹣2)2﹣
(x﹣2)2﹣![]() n,
n,
∴抛物线的对称轴为直线x=2,
∵点A和点B为对称点,
∴2﹣(m﹣2)=2m+3﹣2,解得m=1,
∴A(﹣1,0),B(5,0),
把A(﹣1,0)代入y=﹣![]() [(x﹣2)2+n]得9+n=0,解得n=﹣9;
[(x﹣2)2+n]得9+n=0,解得n=﹣9;
(2)作ND∥y轴交BC于D,如图2,
抛物线解析式为y=﹣![]() [(x﹣2)2﹣9]=﹣
[(x﹣2)2﹣9]=﹣![]() x2+
x2+![]() x+3,
x+3,
当x=0时,y=3,则C(0,3),
设直线BC的解析式为y=kx+b,
把B(5,0),C(0,3)代入得![]() ,解得
,解得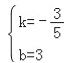 ,
,
∴直线BC的解析式为y=﹣![]() x+3,
x+3,
设N(x,﹣![]() x2+
x2+![]() x+3),则D(x,﹣
x+3),则D(x,﹣![]() x+3),
x+3),
∴ND=﹣![]() x2+
x2+![]() x+3﹣(﹣
x+3﹣(﹣![]() x+3)=﹣
x+3)=﹣![]() x2+3x,
x2+3x,
∴S△NBC=S△NDC+S△NDB=![]() 5ND=﹣
5ND=﹣![]() x2+
x2+![]() x=﹣(x﹣
x=﹣(x﹣![]() )2+
)2+![]() ,
,
当x=![]() 时,△NBC面积最大,最大值为
时,△NBC面积最大,最大值为![]() ;
;
(3)存在.
∵B(5,0),C(0,3),
∴由勾股定理得BC=![]() ,
,
当∠PMB=90°,则∠PMC=90°,△PMC为等腰直角三角形,MP=MC,
设PM=t,则CM=t,MB=![]() ﹣t,
﹣t,
∵∠MBP=∠OBC,
∴△BMP∽△BOC,
∴![]() ,即
,即![]() ,解得t=
,解得t=![]() ,BP=
,BP=![]() ,
,
∴OP=OB﹣BP=5﹣![]() =
=![]() ,
,
此时P点坐标为(![]() ,0);
,0);
当∠MPB=90°,则MP=MC,
设PM=t,则CM=t,MB=![]() ﹣t,
﹣t,
∵∠MBP=∠CBO,
∴△BMP∽△BCO,
∴![]() ,即
,即![]() ,解得t=
,解得t=![]() ,BP=
,BP=![]() ,
,
∴OP=OB﹣BP=5﹣![]() =
=![]() ,
,
此时P点坐标为(![]() ,0);
,0);
综上所述,P点坐标为(![]() ,0)或(
,0)或(![]() ,0).
,0).


科目:初中数学 来源: 题型:
【题目】某文化用品商店计划同时购进一批A、B两种型号的计算器,若购进A型计算器10只和B型计算器8只,共需要资金880元;若购进A型计算器2只和B型计算器5只,共需要资金380只。
(1)求A、B两种型号的计算器每只进价各是多少元?
(2)该经销商计划购进这两种型号的计算器共50只,而可用于购买这两种型号的计算器的资金不超过2520元,根据市场行情,销售一只A型计算器可获利10元,销售一只B型计算器可获利15元,该经销商希望销售完这两种型号的计算器,所获利润不少于620元,则该经销商有哪几种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校篮球队五名主力队员的身高分别是174,179,180,174,178(单位:cm),则这五名队员身高的中位数是( )
A.174cm
B.177cm
C.178cm
D.180cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com