【题目】已知：如图，BE⊥CD，BE＝DE，BC＝DA．

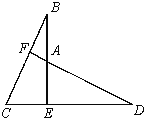
求证：（1）△BEC≌△DAE；

（2）DF⊥BC．

参考答案：

【答案】证明见解析．

【解析】试题分析：此题主要考查学生对全等三角形的判定及性质的理解及运用．全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具．在判定三角形全等时，关键是选择恰当的判定条件．

（1）根据已知利用HL即可判定△BEC≌△DEA；

（2）根据第（1）问的结论，利用全等三角形的对应角相等可得到∠B=∠D，从而不难求得DF⊥BC．

试题解析：证明：（1）∵BE⊥CD，

∴∠BEC=∠DEA=90°，

∴在Rt△BEC与Rt△DEA中，

，

∴△BEC≌△DEA（HL）；

（2）∵由（1）知，△BEC≌△DEA，

∴∠B=∠D．

∵∠D+∠DAE=90°，∠DAE=∠BAF，

∴∠BAF+∠B=90°，即DF⊥BC．

关闭