
����Ŀ���Ķ����⣺
���ǰ�����ij�����������е�����ɵ�ͼ�Σ�����������������ĵ�Ĺ켣��
���磺�ǵ�ƽ�����ǵ��ǵ����߾�����ȵĵ�Ĺ켣��
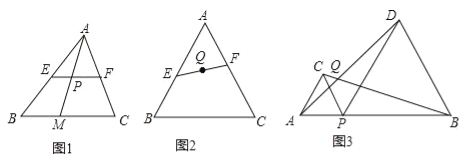
���⣺��ͼ1����֪EFΪ��ABC����λ�ߣ�M�DZ�BC��һ���㣬����AM��EF�ڵ�P����ô����PΪ�߶�AM�е㣮
���ɣ����߶�EFΪ��ABC����λ�ߣ���EF��BC��
��ƽ���߷��߶γɱ����ã�����PΪ�߶�AM�е㣮
�ɴ���õ�����P���˶��켣�ǣ� ��
֪ʶӦ�ã�
��ͼ2����֪EFΪ�ȱ���ABC��AB��AC�ϵĶ��㣬����EF����AF=BE���ҵȱ���ABC�ı߳�Ϊ8�����߶�EF�е�Q���˶��켣�ij���
��չ��ߣ�
��ͼ3��PΪ�߶�AB��һ���㣨��P�����A��B�غϣ������߶�AB��ͬ��ֱ����ȱ���APC�͵ȱ���PBD������AD��BC������ΪQ��
��1������AQB�Ķ�����
��2����AB=6����Q�˶��켣�ij���
���𰸡��Ķ����⣺EF��֪ʶӦ�ã�4����չ��ߣ���1����AQB=120������2������Q�˶��켣�ij�![]() ����
����
��������
����������Ķ����⣺���ݹ켣�Ķ����֪������P���˶��켣���߶�EF��֪ʶӦ�ã���ͼ1�У�����ABC����λ��MN����EG��AC��NM���ӳ�����G��EF��MN���ڵ�Q������GQ��E�ա�NQ��F���Ƴ�Q��Q���غϼ��ɽ�����⣮��չ��ߣ���ͼ2�У���1��ֻҪ֤����APD�ա�CPB���Ƴ���DQG=��BPG=60�����۽�����⣮��2���ɣ�1����֪��P���˶��켣��![]() ���軡AB����Բ��Բ��ΪO��Z Բ������ȡһ��M������AM��BM������M=60������OH��AB��H����AH=BH=3��OH=
���軡AB����Բ��Բ��ΪO��Z Բ������ȡһ��M������AM��BM������M=60������OH��AB��H����AH=BH=3��OH=![]() ��OB=2
��OB=2![]() �����û�����ʽ���ɽ����
�����û�����ʽ���ɽ����
����������Ķ����⣺���ݹ켣�Ķ����֪������P���˶��켣���߶�EF��
֪ʶӦ�ã���ͼ1�У�����ABC����λ��MN����EG��AC��NM���ӳ�����G��EF��MN���ڵ�Q��

�ߡ�ABC�ǵȱ������Σ�MN����λ�ߣ�
��AM=BM=AN=CN��
��AF=BE��
��EM=FN��
��MN��BC��
���AMN=��B=��GME=60����
�ߡ�A=��GEM=60����
���GEM�ǵȱ������Σ�
��EM=EG=FN��
����GQ��E����NQ��F��
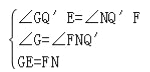 ��
��
���GQ��E�ա�NQ��F��
��EQ��=FQ����
��EQ=QF��
����Q��Q���غϣ�
����Q���߶�MN�ϣ�
����EF�е�Q���˶��켣���߶�MN��
MN=![]() BC=
BC=![]() ��8=4��
��8=4��
���߶�EF�е�Q���˶��켣�ij�Ϊ4��
��չ��ߣ���ͼ2�У�

��1���ߡ�APC����PBD���ǵȱ������Σ�
��AP=PC��PD=PB����APC=��DPB=60����
���APD=��CPB��
����APD����CPB��
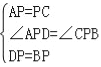 ��
��
���APD�ա�CPB��
���ADP=��CBP����BC��PD���ڵ�G��
�ߡ�QGD=��PGB��
���DQG=��BPG=60����
���AQB=180�㩁��DQG=120��
��2���ɣ�1����֪��P���˶��켣��![]() ���軡AB����Բ��Բ��ΪO��Z Բ������ȡһ��M������AM��BM������M=60����
���軡AB����Բ��Բ��ΪO��Z Բ������ȡһ��M������AM��BM������M=60����
���AOB=2��M=120������OH��AB��H����AH=BH=3��OH=![]() ��OB=2
��OB=2![]() ��
��
����AB�ij�=![]() =
=![]() ����
����
������Q�˶��켣�ij�![]() ����
����


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУ������ȤС�������ͬѧ��һ������ѵ���У�������ŵĴ����ֱ�Ϊ��6��7��7��8��9���������ݵ�����Ϊ�� ��
A.6
B.7
C.8
D.9
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪m��6���෴����n��m���෴��С2����m-n����( )
A. 4 B. 8 C. -2 D. -10
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ������˵ĸ߶�,����ȡ1�׳���ľ��ֱ����������,��Ӱ��Ϊ1.5��,��ͬһʱ�̲����˵�Ӱ��Ϊ10.5��,����˵ĸ߶���____��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͳ�ƣ�2015�������й�ҵ�ܲ�ֵ��4573�ڣ���4573�ÿ�ѧ��������ʾΪ�� ��
A.4.573��103
B.45.73��102
C.4.573��104
D.0.4573��104
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��ͬѧ�ڲμӽ��������п�ǰ�����������ѵ�������7�ε�ѵ���ɼ�����Ϊ��41��43��43��44��45��45��45����ô�������ݵ���λ���ǣ� ��
A.41
B.43
C.44
D.45
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����������ͯ��װ���⣬�ڡ���һ����һ������������У�ij���ͯװÿ����60Ԫ�ļ۸�������ӯ��20%�������ֹ��ͯװÿ���Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABΪ��O��ֱ����ֱ��CD����O�ڵ�M��BE��CD�ڵ�E��
��1����֤����BME=��MAB��
��2����֤��BM2=BEAB��
��3����BE=![]() ��sin��BAM=
��sin��BAM=![]() �����߶�AM�ij���
�����߶�AM�ij���

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com