练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．已知，线段AB=12，点O是AB的中点，C是线段AO上一点，且OC：OB=1：3，求线段AC的长．

    分析 根据中点定义求出OB，由OC、OB之间的关系求出OC，再由AC=AO-CO求出AC．

    解答 解：∵O是AB中点，AB=12，
    ∴AO=OB=6，
    ∵OC：OB=1：3，
    ∴OC=2，
    ∴AC=AO-OC=6-2=4．

    点评 本题考查中点定义，线段和差倍数关系，搞清楚线段之间的关系是解决这类题目的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    11．先化简（1+$\frac{1}{a-1}$）÷$\frac{{a}^{2}+a}{1-a}$，再从1，2中选取一个适当的数代入求值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．如图，在半径为5cm的⊙O中，弦AB=6cm，OC⊥AB于点C，则OC的值为（　　）
    A．6cmB．5cmC．4cmD．3cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．如图，将△ABC纸片折叠，使点A落在边BC上，记落点为点D，且折痕EF∥BC，若EF=3，则BC的长度为6．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．2015年下半年，便民超市某商品的月销量分别是：200，500，350，300，600，350，则这六个数据的中位数是（　　）
    A．600B．350C．325D．300

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

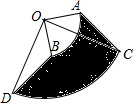    6．如图，将圆心角都是90°的扇形OAB和扇形OCD叠放在一起，连接AC、BD．
    （1）将△AOC经过怎样的图形变换可以得到△BOD？
    （2）若$\widehat{AB}$的长为πcm，OD=3cm，求图中阴影部分的面积是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．某厂生产A、B两种产品，其单价随市场变化而做相应调整，营销人员根据前三次单价变化的情况，绘制了如下统计表及不完整的折线图：
    第一次第二次第三次
    A产品单价（元/件）65.26.5
    B产品单价（元/件）3.543
    并求得了A产品三次单价的平均数和方差：
    $\overline{{x}_{A}}=5.9$；SA2=$\frac{1}{3}$[（6-5.9）2+（5.2-5.9）2+（6.5-5.9）2]=$\frac{43}{150}$
    （1）补全“A、B产品单价变化的折线图”，B产品第三次的单价比上一次的单价降低了百分之多少？
    （2）求B产品三次单价的方差，并比较哪种产品的单价波动小；
    （3）该厂决定第四次调价，A产品的单价仍为6.5元/件．
    则A产品这四次单价的中位数是6.25元/件．
    若A产品这四次单价的中位数是B产品四次单价中位数的2倍少1，则B产品的第四次单价为3.75元/件．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．如图，四边形ABCD内接于⊙O，若⊙O的半径为6，∠A=130°，则扇形OBAD的面积为10π．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．如图，在△ABC中，∠C=90°，∠A=30°，边AB的垂直平分线DE交AC于D，若CD=3cm，则AC=9cm．

    查看答案和解析>>

    同步练习册答案