
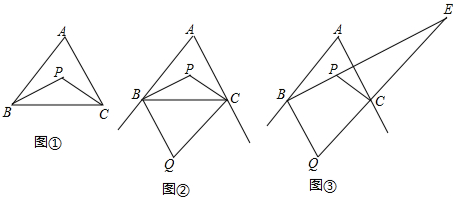
分析 (1)运用三角形的内角和定理及角平分线的定义,首先求出∠1+∠2,进而求出∠BPC即可解决问题;
(2)根据三角形的外角性质分别表示出∠MBC与∠BCN,再根据角平分线的性质可求得∠CBQ+∠BCQ,最后根据三角形内角和定理即可求解;
(3)在△BQE中,由于∠Q=90°-$\frac{1}{2}$∠A,求出∠E=$\frac{1}{2}$∠A,∠EBQ=90°,所以如果△BQE中,存在一个内角等于另一个内角的2倍,那么分四种情况进行讨论:①∠EBQ=2∠E=90°;②∠EBQ=2∠Q=90°;③∠Q=2∠E;④∠E=2∠Q;分别列出方程,求解即可.
解答 解:(1)如图①,
∵在△ABC中,∠A+∠ABC+∠ACB=180°,且∠A=80°,
∴∠ABC+∠ACB=100°,
∵∠1=$\frac{1}{2}$∠ABC,∠2=$\frac{1}{2}$∠ACB,
∴∠1+∠2=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$×100°=50°,
∴∠BPC=180°-(∠1+∠2)=180°-50°=130°.
(2)如图②,
∵∠MBC=∠A+∠ACB,∠BCN=∠ABC+∠A,
∴∠MBC+∠BCN=∠A+∠ABC+∠ACB+∠A=180°+∠A.
∵BE,CQ分别为△ABC的外角∠MBC,∠NCB的角平分线,
∴∠CBQ+∠BCQ=$\frac{1}{2}$(180°+∠A),
∴∠Q=180°-(∠CBQ+∠BCQ)=90°-$\frac{1}{2}$∠A;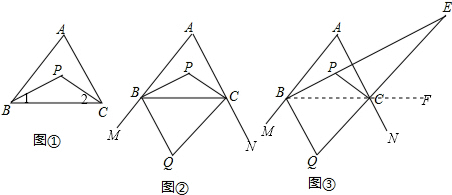 (3)如图③,连结BC并延长到点F.
(3)如图③,连结BC并延长到点F.
∵CQ为△ABC的外角∠NCB的角平分线,
∴CE是△ABC的外角∠ACF的平分线,
∴∠ACF=2∠ECF,
∵BE平分∠ABC,
∴∠ABC=2∠EBC,
∵∠ECF=∠EBC+∠E,
∴2∠ECF=2∠EBC+2∠E,
即∠ACF=∠ABC+2∠E,
又∵∠ACF=∠ABC+∠A,
∴∠A=2∠E,即∠E=$\frac{1}{2}$∠A;
∵∠EBQ=∠EBC+∠CBQ
=$\frac{1}{2}$∠ABC+$\frac{1}{2}$∠MBC
=$\frac{1}{2}$(∠ABC+∠A+∠ACB)=90°.
如果△BQE中,存在一个内角等于另一个内角的2倍,那么分四种情况:
①∠EBQ=2∠E=90°,则∠E=45°,∠A=2∠E=90°;
②∠EBQ=2∠Q=90°,则∠Q=45°,∠E=45°,∠A=2∠E=90°;
③∠Q=2∠E,则90°-$\frac{1}{2}$∠A=∠A,解得∠A=60°;
④∠E=2∠Q,则$\frac{1}{2}$∠A=2(90°-$\frac{1}{2}$∠A),解得∠A=120°.
综上所述,∠A的度数是90°或60°或120°.
点评 本题是三角形综合题,考查了三角形内角和定理、外角的性质,角平分线定义等知识;灵活运用三角形的内角和定理、外角的性质进行分类讨论是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
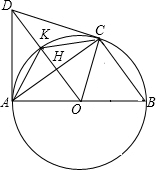 AB是⊙O的直径,CD与⊙O相切于点C,DA⊥AB,DO及DO的延长线与⊙O分别相交于点E,F,EB与CF相交点G,⊙O的半径为3,DC=4,求CH,OH,HK,DK,CK的长及BC的长.
AB是⊙O的直径,CD与⊙O相切于点C,DA⊥AB,DO及DO的延长线与⊙O分别相交于点E,F,EB与CF相交点G,⊙O的半径为3,DC=4,求CH,OH,HK,DK,CK的长及BC的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中xOy中,边长为10的正方形ABCD的对角线AC,BD相交于点P,点A在x轴正半轴上运动,点B在y轴正半轴上运动(正半轴不包含原点O),点C、D都在第一象限.
如图,在平面直角坐标系中xOy中,边长为10的正方形ABCD的对角线AC,BD相交于点P,点A在x轴正半轴上运动,点B在y轴正半轴上运动(正半轴不包含原点O),点C、D都在第一象限.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
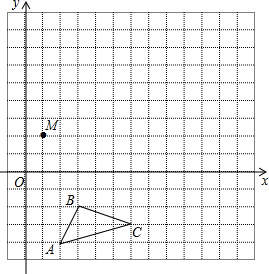 在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,-4),B(3,-2),C(6,-3).
在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,-4),B(3,-2),C(6,-3).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com