
| A. | 13 | B. | $\frac{13}{2}\sqrt{2}$ | C. | $\frac{17}{2}\sqrt{2}$ | D. | 12 |
分析 ①CD是平行四边形的一条边,那么有AB=CD;②CD是平行四边形的一条对角线,过C作CM⊥AO于M,过D作DF⊥AO于F,交AC于Q,过B作BN⊥DF于N,证△DBN≌△CAM,推出DN=CM=a,BN=AM=-5-a,得出D((5+a,12-a),由勾股定理得:CD2=(5+a+a)2+(12-a-a)2=8(a-$\frac{7}{4}$)2+$\frac{289}{2}$,当a=$\frac{7}{4}$时,CD有最小值,是$\frac{17\sqrt{2}}{2}$.
解答 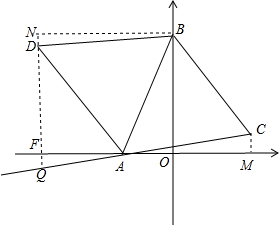 解:有两种情况:
解:有两种情况:
①CD是平行四边形的一条边,那么有AB=CD=$\sqrt{{(-5)}^{2}{+12}^{2}}$=13,
②CD是平行四边形的一条对角线,
过C作CM⊥AO于M,过D作DF⊥AO于F,交AC于Q,过B作BN⊥DF于N,
则∠BND=∠DFA=∠CMA=∠QFA=90°,
∠CAM+∠FQA=90°,∠BDN+∠DBN=90°,
∵四边形ACBD是平行四边形,
∴BD=AC,∠C=∠D,BD∥AC,
∴∠BDF=∠FQA,
∴∠DBN=∠CAM,
∵在△DBN和△CAM中$\left\{\begin{array}{l}{∠BND=∠AMC}\\{∠DBN=∠CAM}\\{BD=AC}\end{array}\right.$
∴△DBN≌△CAM(AAS),
∴DN=CM=a,BN=AM=a+5,
∴D(-5-a,12-a),
由勾股定理得:CD2=(5+a+a)2+(12-a-a)2=8(a-$\frac{7}{4}$)2+$\frac{289}{2}$,当a=$\frac{7}{4}$时,CD有最小值,是$\frac{17\sqrt{2}}{2}$,
∵$\frac{17\sqrt{2}}{2}$<13,
∴CD的最小值是$\frac{17\sqrt{2}}{2}$.
故选C.
点评 本题考查了平行四边形性质,全等三角形的性质和判定,二次函数的最值的应用,关键是能得出关于a的二次函数解析式,题目比较好,难度偏大.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:选择题
| A. | 8.5、0.7 | B. | 8.5、1.7 | C. | 8.0、0.7 | D. | 8.0、1.7 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 34 | B. | 43 | C. | 25 | D. | 52 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
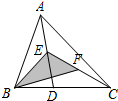 如图,在△ABC中,已知点E、F分别是AD、CE边上的中点,且S△BEF=4cm2,则S△ABC的值为( )
如图,在△ABC中,已知点E、F分别是AD、CE边上的中点,且S△BEF=4cm2,则S△ABC的值为( )| A. | 1cm2 | B. | 2cm2 | C. | 8cm2 | D. | 16cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
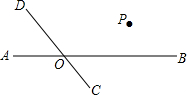 如图,直线CD与直线AB相交于O,根据下列语句画图:
如图,直线CD与直线AB相交于O,根据下列语句画图:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2m3+3m2=5m5 | B. | -5(-x3)-2=-$\frac{5}{{x}^{6}}$ | C. | (3a3b3)2=6a6b6 | D. | $\sqrt{(-2)^{2}}$=-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC内接于⊙O,AB为直径,点D在⊙O上,过点D作⊙O切线与AC的延长线交于点E,ED∥BC,连接AD交BC于点F.
如图,△ABC内接于⊙O,AB为直径,点D在⊙O上,过点D作⊙O切线与AC的延长线交于点E,ED∥BC,连接AD交BC于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com