
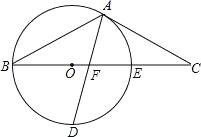
【题目】如图,以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,AC=FC.
(1)求证:AC是⊙O的切线;
(2)已知圆的半径R=5,EF=3,求DF的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)连结OA、OD,如图,根据垂径定理的推理,由D为BE的下半圆弧的中点得到OD⊥BE,则∠D+∠DFO=90°,再由AC=FC得到∠CAF=∠CFA,根据对顶角相等得∠CFA=∠DFO,所以∠CAF=∠DFO,加上∠OAD=∠ODF,则∠OAD+∠CAF=90°,于是根据切线的判定定理即可得到AC是⊙O的切线;
(2)由于圆的半径R=5,EF=3,则OF=2,然后在Rt△ODF中利用勾股定理计算DF的长.
试题解析:(1)连结OA、OD,如图,
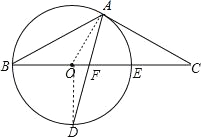
∵D为BE的下半圆弧的中点,
∴OD⊥BE,
∴∠D+∠DFO=90°,
∵AC=FC,
∴∠CAF=∠CFA,
∵∠CFA=∠DFO,
∴∠CAF=∠DFO,
而OA=OD,
∴∠OAD=∠ODF,
∴∠OAD+∠CAF=90°,即∠OAC=90°,
∴OA⊥AC,
∴AC是⊙O的切线;
(2)∵圆的半径R=5,EF=3,
∴OF=2,
在Rt△ODF中,∵OD=5,OF=2,
∴DF=![]() .
.


科目:初中数学 来源: 题型:
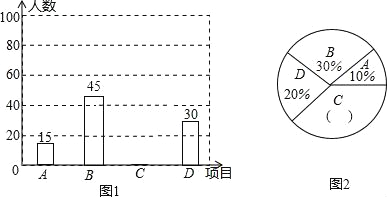
【题目】为进一步推广“阳光体育”大课间活动,某中学对已开设的A实心球,B立定跳远,C跑步,D跳绳四种活动项目的学生喜欢情况进行调查,随机抽取了部分学生,并将调查结果绘制成图1,图2的统计图,请结合图中的信息解答下列问题:
(1)请计算本次调查中喜欢“跑步”的学生人数和所占百分比,并将两个统计图补充完整;
(2)随机抽取了5名喜欢“跑步”的学生,其中有3名女生,2名男生,现从这5名学生中任意抽取2名学生,请用画树状图或列表的方法,求出刚好抽到同性别学生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分7分)完成下列各题:
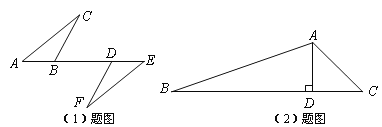
(1)如图,点A,B,D,E在同一直线上,AB=ED,AC∥EF,∠C=∠F.求证:AC=EF.
(2)如图,在△ABC中,AD是BC边上的高,∠C=45°,sinB=![]() ,AD=1.求BC的长.
,AD=1.求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
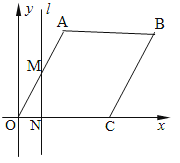
【题目】如图,在平面直角坐标系中,四边形OABC是菱形,点C的坐标为(4,0),∠AOC=60°,垂直于![]() 轴的直线l从
轴的直线l从![]() 轴出发,沿
轴出发,沿![]() 轴正方向以每秒1个单位长度的速度向右平移,设直线l与菱形OABC的两边分别交于点M,N(点M在点N的上方),若△OMN的面积为S,直线l的运动时间为t 秒。试问:S与t的函数关析式?
轴正方向以每秒1个单位长度的速度向右平移,设直线l与菱形OABC的两边分别交于点M,N(点M在点N的上方),若△OMN的面积为S,直线l的运动时间为t 秒。试问:S与t的函数关析式?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com