
【题目】小平所在的学习小组发现,车辆转弯时,能否顺利通过直角弯道的标准是,车辆是否可以行驶到和路的边界夹角是45°的位置(如图1中 ②的位置).例如,图2是某巷子的俯视图,巷子路面宽4m,转弯处为直角,车辆的车身为矩形ABCD,CD与DE、CE的夹角都是45°时,连接EF,交CD于点G,若GF的长度至少能达到车身宽度,即车辆能通过.
(1)小平认为长8m,宽3m的消防车不能通过该直角转弯,请你帮他说明理由;
(2)小平提出将拐弯处改为圆弧( ![]() 和
和 ![]() 是以O为圆心,分别以OM和ON为半径的弧),长8m,宽3m的消防车就可以通过该弯道了,具体的方案如图,其中OM⊥OM′,你能帮小平算出,ON至少为多少时,这种消防车可以通过该巷子?
是以O为圆心,分别以OM和ON为半径的弧),长8m,宽3m的消防车就可以通过该弯道了,具体的方案如图,其中OM⊥OM′,你能帮小平算出,ON至少为多少时,这种消防车可以通过该巷子?
【答案】
(1)
解:消防车不能通过该直角转弯.
理由如下:如图,作FH⊥EC,垂足为H,

∵FH=EH=4,
∴EF=4 ![]() ,且∠GEC=45°,
,且∠GEC=45°,
∵GC=4,
∴GE=GC=4,
∴GF=4 ![]() ﹣4<3,
﹣4<3,
即GF的长度未达到车身宽度,
∴消防车不能通过该直角转弯;
(2)解:若C、D分别与M′、M重合,则△OGM为等腰直角三角形,
∴OG=4,OM=4 ![]() ,
,
∴OF=ON=OM﹣MN=4 ![]() ﹣4,
﹣4,
∴FG=OG﹣OF= ![]() ×8﹣(4
×8﹣(4 ![]() ﹣4)=8﹣4
﹣4)=8﹣4 ![]() <3,
<3,
∴C、D在 ![]() 上,
上,
设ON=x,连接OC,在Rt△OCG中,
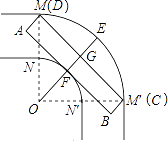
OG=x+3,OC=x+4,CG=4,
由勾股定理得,OG2+CG2=OC2,
即(x+3)2+42=(x+4)2,
解得x=4.5.
答:ON至少为4.5米.
【解析】(1)过点F作FH⊥EC于点H,根据道路的宽度求出FH=EH=4m,然后根据等腰直角三角形的性质求出EF、GE的长度,相减即可得到GF的长度,如果不小于车身宽度,则消防车能通过,否则,不能通过;(2)假设车身C、D分别与点M′、M重合,根据等腰直角三角形的性质求出OG= ![]() CD=4,OC=
CD=4,OC= ![]() CG=4
CG=4 ![]() ,然后求出OF的长度,从而求出可以通过的车宽FG的长度,如果不小于车宽,则消防车能够通过,否则,不能通过;设ON=x,表示出OC=x+4,OG=x+3,又OG=
,然后求出OF的长度,从而求出可以通过的车宽FG的长度,如果不小于车宽,则消防车能够通过,否则,不能通过;设ON=x,表示出OC=x+4,OG=x+3,又OG= ![]() CD=4,在Rt△OCG中,利用勾股定理列式进行计算即可求出ON的最小值.
CD=4,在Rt△OCG中,利用勾股定理列式进行计算即可求出ON的最小值.


科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则正比例函数y=(b+c)x与反比例函数y= ![]() 在同一坐标系中的大致图象是( )
在同一坐标系中的大致图象是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=kx+b与反比例函数y= ![]() (x>0)的图象分别交于点 A(m,3)和点B(6,n),与坐标轴分别交于点C和点D.
(x>0)的图象分别交于点 A(m,3)和点B(6,n),与坐标轴分别交于点C和点D.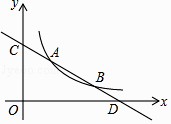
(1)求直线AB的解析式;
(2)若点P是x轴上一动点,当△COD与△ADP相似时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CD是AB边上的中线,E是CD的中点,过点C作AB的平行线交AE的延长线于点F,连接BF. 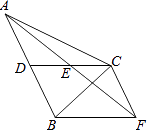
(1)求证:CF=AD;
(2)若CA=CB,∠ACB=90°,试判断四边形CDBF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在梯形ABCD中,AB∥CD,E是BC的中点,EF⊥AD于点F,AD=4,EF=5,则梯形ABCD的面积是( ) 
A.40
B.30
C.20
D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若记y=f(x)= ![]() ,其中f(1)表示当x=1时y的值, 即f(1)=
,其中f(1)表示当x=1时y的值, 即f(1)= ![]() =
= ![]() ;f(
;f( ![]() )表示当x=
)表示当x= ![]() 时y的值,即f(
时y的值,即f( ![]() )=
)= ![]()
![]() ;…;则f(1)+f(2)+f(
;…;则f(1)+f(2)+f( ![]() )+f(3)+f(
)+f(3)+f( ![]() )+…+f(2011)+f(
)+…+f(2011)+f( ![]() )= .
)= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的面积是63,D是BC上的一点,且BD:CD=2:1,DE∥AC交AB于E,延长DE到F,使FE:ED=2:1,则△CDF的面积是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的四个顶点在坐标轴上,A点坐标为(3,0),假设有甲、乙两个物体分别由点A同时出发,沿正方形ABCD的边作环绕运动,物体甲按逆时针方向匀速运动,物体乙按顺时针方向匀速运动,如果甲物体12秒钟可环绕一周回到A点,乙物体24秒钟可环绕一周回到A点,则两个物体运动后的第2017次相遇地点的坐标是( )
A.(3,0)
B.(﹣1,2)
C.(﹣3,0)
D.(﹣1,﹣2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com