
【题目】如图,△ABC的面积是63,D是BC上的一点,且BD:CD=2:1,DE∥AC交AB于E,延长DE到F,使FE:ED=2:1,则△CDF的面积是 . 
【答案】42
【解析】方法一: 解:连接CE,
因为BD:CD=2:1,所以△BDE和△CDE的面积之比为2:1,
又因为DE∥AC,
∴ ![]() =
= ![]() ,
,
∴S△BDE:S△ABC=4:9,
又因为△ABC的面积是63,
∴△BDE的面积为:28,
所以△CDE的面积为14,
因为FE:ED=2:1,所以△FDC和△CDE的面积之比为3:1
所以答案是:42.
方法二:解:作MW⊥BC,AN⊥BC,垂足分别为W,N.
∵BD:CD=2:1,DE∥AC,
∴BE:AE=2:1,
∴BD:BC=DE:AC=BE:AB=2:3,
∴S△BDE:S△ABC=4:9,
∴S△BDE= ![]() ×63=28,
×63=28,
∵FE:ED=2:1=4:2,
∴EF:AC=4:3,
∴S△MEF:S△AMC=16:9,
∴EM:AM=4:3,
假设EM=4x,AM=3x,BE= ![]() AB=2AE=2(EM+AM)=14x,
AB=2AE=2(EM+AM)=14x,
∴BM:AM=18x:3x=18:3,
∴MW:AN=BM:AB=18:21=6:7,
∴S△BMC:S△ABC= ![]() BCWM:
BCWM: ![]() BCAN=WM:AN=6:7,
BCAN=WM:AN=6:7,
∵S△ABC=63,
∴S△BMC=54,
∴S△AMC=63﹣54=9,
∵S△MEF:S△AMC=16:9,
∴S△MEF=16,
∵S△BDE= ![]() ×63=28,
×63=28,
∴S四边形MEDC=63﹣9﹣28=26,
∴△CDF的面积是:26+16=42.
所以答案是:42.
【考点精析】关于本题考查的三角形的面积和平行线分线段成比例,需要了解三角形的面积=1/2×底×高;三条平行线截两条直线,所得的对应线段成比例才能得出正确答案.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣ ![]() x+
x+ ![]() 分别与x轴、y轴交于B、C两点,点A在x轴上,∠ACB=90°,抛物线y=ax2+bx+
分别与x轴、y轴交于B、C两点,点A在x轴上,∠ACB=90°,抛物线y=ax2+bx+ ![]() 经过A,B两点.
经过A,B两点.
(1)求A、B两点的坐标;
(2)求抛物线的解析式;
(3)点M是直线BC上方抛物线上的一点,过点M作MH⊥BC于点H,作MD∥y轴交BC于点D,求△DMH周长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小平所在的学习小组发现,车辆转弯时,能否顺利通过直角弯道的标准是,车辆是否可以行驶到和路的边界夹角是45°的位置(如图1中 ②的位置).例如,图2是某巷子的俯视图,巷子路面宽4m,转弯处为直角,车辆的车身为矩形ABCD,CD与DE、CE的夹角都是45°时,连接EF,交CD于点G,若GF的长度至少能达到车身宽度,即车辆能通过.
(1)小平认为长8m,宽3m的消防车不能通过该直角转弯,请你帮他说明理由;
(2)小平提出将拐弯处改为圆弧( ![]() 和
和 ![]() 是以O为圆心,分别以OM和ON为半径的弧),长8m,宽3m的消防车就可以通过该弯道了,具体的方案如图,其中OM⊥OM′,你能帮小平算出,ON至少为多少时,这种消防车可以通过该巷子?
是以O为圆心,分别以OM和ON为半径的弧),长8m,宽3m的消防车就可以通过该弯道了,具体的方案如图,其中OM⊥OM′,你能帮小平算出,ON至少为多少时,这种消防车可以通过该巷子?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在以O为圆心的两个同心圆中,小圆的半径为1,AB与小圆相切于点A,与大圆相交于点B,大圆的弦BC⊥AB于点B,过点C作大圆的切线CD交AB的延长线于点D,连接OC交小圆于点E,连接BE、BO. 
(1)求证:△AOB∽△BDC;
(2)设大圆的半径为x,CD的长为y: ①求y与x之间的函数关系式;
②当BE与小圆相切时,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园手机”现象越来越受到社会的关注.小丽在“统计实习”活动中随机调查了学校若干名学生家长对“中学生带手机到学校”现象的看法,统计整理并制作了如下的统计图: 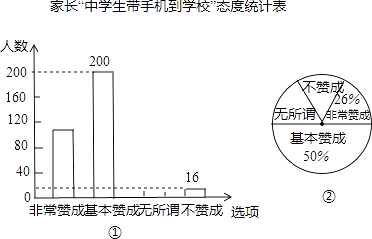
(1)求这次调查的家长总数及家长表示“无所谓”的人数,并补全图①;
(2)求图②中表示家长“无所谓”的圆心角的度数;
(3)从这次接受调查的家长中,随机抽查一个,恰好是“不赞成”态度的家长的概率是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=1,BC=2,BC在x轴上,一次函数y=kx﹣2的图象经过A、C两点,并与y轴交于点E,反比例函数y= ![]() 的图象经过点A.
的图象经过点A.
(1)写出点E的坐标;
(2)求一次函数和反比例函数的解析式;
(3)根据图象写出当x>0时,一次函数的值大于反比例函数的值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,正方形A1B1C1D1、D1 E1E2B2、A2B2 C2D2、D2E3E4B3…按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3…在x轴上,已知正方形A1B1C1D1的边长为l,∠B1C1O=60°,B1C1∥B2C2∥B3C3…,则正方形A2017B2017C2017 D2017的边长是( ) 
A.( ![]() )2016
)2016
B.( ![]() )2017
)2017
C.( ![]() )2016
)2016
D.( ![]() )2017
)2017
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,∠A=90°,BC=4,点P是△ABC边上一动点,沿B→A→C的路径移动,过点P作PD⊥BC于点D,设BD=x,△BDP的面积为y,则下列能大致反映y与x函数关系的图象是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后,折痕DE分别交AB,AC于点E、G,连接GF,有下列结论: ①∠AGD=112.5°;②tan∠AED= ![]() +1;③四边形AEFG是菱形;④S△ACD=
+1;③四边形AEFG是菱形;④S△ACD= ![]() S△OCD .
S△OCD .
其中正确结论的序号是 . (把所有正确结论的序号都填在横线上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com