
【题目】如图,直线y=﹣ ![]() x+
x+ ![]() 分别与x轴、y轴交于B、C两点,点A在x轴上,∠ACB=90°,抛物线y=ax2+bx+
分别与x轴、y轴交于B、C两点,点A在x轴上,∠ACB=90°,抛物线y=ax2+bx+ ![]() 经过A,B两点.
经过A,B两点.
(1)求A、B两点的坐标;
(2)求抛物线的解析式;
(3)点M是直线BC上方抛物线上的一点,过点M作MH⊥BC于点H,作MD∥y轴交BC于点D,求△DMH周长的最大值.
【答案】
(1)
解:∵直线y=﹣ ![]() x+
x+ ![]() 分别与x轴、y轴交于B、C两点,
分别与x轴、y轴交于B、C两点,
∴B(3,0),C(0, ![]() ),
),
∴OB=3,OC= ![]() ,
,
∴tan∠BCO= ![]() =
= ![]() ,
,
∴∠BCO=60°,
∵∠ACB=90°,
∴∠ACO=30°,
∴ ![]() =tan30°=
=tan30°= ![]() ,即
,即 ![]() =
= ![]() ,解得AO=1,
,解得AO=1,
∴A(﹣1,0);
(2)
解:∵抛物线y=ax2+bx+ ![]() 经过A,B两点,
经过A,B两点,
∴ ![]() ,解得
,解得 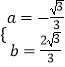 ,
,
∴抛物线解析式为y=﹣ ![]() x2+
x2+ ![]() x+
x+ ![]() ;
;
(3)
解:∵MD∥y轴,MH⊥BC,
∴∠MDH=∠BCO=60°,则∠DMH=30°,
∴DH= ![]() DM,MH=
DM,MH= ![]() DM,
DM,
∴△DMH的周长=DM+DH+MH=DM+ ![]() DM+
DM+ ![]() DM=
DM= ![]() DM,
DM,
∴当DM有最大值时,其周长有最大值,
∵点M是直线BC上方抛物线上的一点,
∴可设M(t,﹣ ![]() t2+
t2+ ![]() t+
t+ ![]() ),则D(t,﹣
),则D(t,﹣ ![]() t+
t+ ![]() ),
),
∴DM=﹣ ![]() t2+
t2+ ![]() t+
t+ ![]() ),则D(t,﹣
),则D(t,﹣ ![]() t+
t+ ![]() ),
),
∴DM=﹣ ![]() t2+
t2+ ![]() t+
t+ ![]() ﹣(﹣
﹣(﹣ ![]() t+
t+ ![]() )=﹣
)=﹣ ![]() t2+
t2+ ![]() t=﹣
t=﹣ ![]() (t﹣
(t﹣ ![]() )2+
)2+ ![]() ,
,
∴当t= ![]() 时,DM有最大值,最大值为
时,DM有最大值,最大值为 ![]() ,
,
此时 ![]() DM=
DM= ![]() ×
× ![]() =
= ![]() ,
,
即△DMH周长的最大值为 ![]() .
.
【解析】(1)由直线解析式可求得B、C坐标,在Rt△BOC中由三角函数定义可求得∠OCB=60°,则在Rt△AOC中可得∠ACO=30°,利用三角函数的定义可求得OA,则可求得A点坐标;(2)由A、B两点坐标,利用待定系数法可求得抛物线解析式;(3)由平行线的性质可知∠MDH=∠BCO=60°,在Rt△DMH中利用三角函数的定义可得到DH、MH与DM的关系,可设出M点的坐标,则可表示出DM的长,从而可表示出△DMH的周长,利用二次函数的性质可求得其最大值.
【考点精析】通过灵活运用二次函数的最值和平行线的性质,掌握如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a;两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补即可以解答此题.


科目:初中数学 来源: 题型:
【题目】如图,在等腰直角△ABC中,∠ACB=90°,点D为三角形内一点,且∠ACD=∠DAB=∠DBC. 
(1)求∠CDB的度数;
(2)求证:△DCA∽△DAB;
(3)若CD的长为1,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则正比例函数y=(b+c)x与反比例函数y= ![]() 在同一坐标系中的大致图象是( )
在同一坐标系中的大致图象是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B两地相距60km,甲、乙两人从两地出发相向而行,甲先出发,图中l1 , l2表示两人离A地的距离s(km)与时间t(h)的关系,请结合图象解答下列问题: 
(1)表示乙离A地的距离与时间关系的图象是(填l1或l2); 甲的速度是km/h,乙的速度是km/h;
(2)甲出发多少小时两人恰好相距5km?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明从家到学校,先匀速步行到车站,等了几分钟后坐上了公交车,公交车沿着公路匀速行驶一段时间后到达学校,小明从家到学校行驶路程s(m)与时间t(min)的大致图象是( )
A.
B.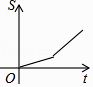
C.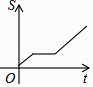
D.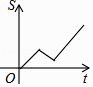
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为大力弘扬“奉献、友爱、互助、进步”的志愿服务精神,传播“奉献他人、提升自我”的志愿服务理念,东营市某中学利用周末时间开展了“助老助残、社区服务、生态环保、网络文明”四个志愿服务活动(每人只参加一个活动),九年级某班全班同学都参加了志愿服务,班长为了解志愿服务的情况,收集整理数据后,绘制以下不完整的统计图,请你根据统计图中所提供的信息解答下列问题: 
(1)求该班的人数;
(2)请把折线统计图补充完整;
(3)求扇形统计图中,网络文明部分对应的圆心角的度数;
(4)小明和小丽参加了志愿服务活动,请用树状图或列表法求出他们参加同一服务活动的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=kx+b与反比例函数y= ![]() (x>0)的图象分别交于点 A(m,3)和点B(6,n),与坐标轴分别交于点C和点D.
(x>0)的图象分别交于点 A(m,3)和点B(6,n),与坐标轴分别交于点C和点D.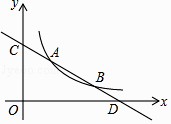
(1)求直线AB的解析式;
(2)若点P是x轴上一动点,当△COD与△ADP相似时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的面积是63,D是BC上的一点,且BD:CD=2:1,DE∥AC交AB于E,延长DE到F,使FE:ED=2:1,则△CDF的面积是 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com