
分析 ①分子、分母都乘以$\sqrt{15}$+3,再加以化简可得;
②将分子5拆成12-7=($\sqrt{12}+\sqrt{7}$)($\sqrt{12}-\sqrt{7}$)=(2$\sqrt{3}+\sqrt{7}$)(2$\sqrt{3}-\sqrt{7}$),再约分可得.
解答 解:①$\frac{2}{\sqrt{15}-3}$=$\frac{2(\sqrt{15}+3)}{(\sqrt{15}-3)(\sqrt{15}+3)}$=$\frac{2(\sqrt{15}+3)}{15-9}$=$\frac{\sqrt{15}+3}{3}$;
②$\frac{5}{2\sqrt{3}+\sqrt{7}}$=$\frac{12-7}{2\sqrt{3}+\sqrt{7}}$=$\frac{(\sqrt{12}+\sqrt{7})(\sqrt{12}-\sqrt{7})}{2\sqrt{3}+\sqrt{7}}$=$\frac{(2\sqrt{3}+\sqrt{7})(2\sqrt{3}-\sqrt{7})}{2\sqrt{3}+\sqrt{7}}$=2$\sqrt{3}$-$\sqrt{7}$.
点评 本题主要考查分母有理化,理解题意掌握分母有理化的不同方法是解题的关键.


科目:初中数学 来源: 题型:解答题
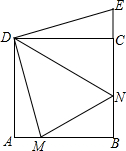 如图,在正方形ABCD中,AB=4,∠MDN=45°,点M,N分别在AB,BC边上,延长BC至E,使CE=AM,连接DE.
如图,在正方形ABCD中,AB=4,∠MDN=45°,点M,N分别在AB,BC边上,延长BC至E,使CE=AM,连接DE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4的算术平方根是±2 | B. | $\sqrt{81}$的平方根是±3 | ||
| C. | 8的立方根是2 | D. | 立方根等于-1的实数是-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
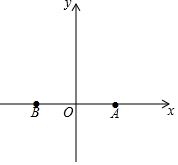 如图,在平面直角坐标系中,点A的坐标为(2,0),点A关于y轴的对称点为点B.
如图,在平面直角坐标系中,点A的坐标为(2,0),点A关于y轴的对称点为点B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com