
【题目】如图,点O是直线AB上任一点,射线OD和射线OE分别平分∠AOC和∠BOC. 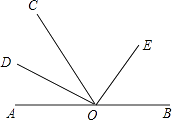
(1)与∠AOE互补的角是 .
(2)若∠AOC=72°,求∠DOE的度数;
(3)当∠AOC=x时,请直接写出∠DOE的度数.
【答案】
(1)∠BOE、∠COE
(2)解:∵OD、OE分别平分∠AOC、∠BOC,∠AOC=72°,
∴∠COD=∠AOD=36°,∠COE=∠BOE= ![]() ∠BOC,
∠BOC,
∴∠BOC=180°﹣72°=108°,
∴∠COE= ![]() ∠BOC=54°,
∠BOC=54°,
∴∠DOE=∠COD+∠COE=90°
(3)解:当∠AOD=x°时,∠DOE=90°
【解析】解:(1)∵OE平分∠BOC,
∴∠BOE=∠COE;
∵∠AOE+∠BOE=180°,
∴∠AOE+∠COE=180°,
∴与∠AOE互补的角是∠BOE、∠COE;
所以答案是∠BOE、∠COE;
【考点精析】本题主要考查了余角和补角的特征的相关知识点,需要掌握互余、互补是指两个角的数量关系,与两个角的位置无关才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】下列说法中,不正确的是( )
A.同位角相等,两直线平行;
B.两直线平行,内错角相等;
C.两直线被第三条直线所截,同旁内角互补;
D.同旁内角互补,两直线平行
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某通讯公司推出①,②两种通讯收费方式供用户选择,其中一种有月租费,另一种无月租费,且两种收费方式的通讯时间x(分)与费用y(元)之间的函数关系如图所示.
(1)有月租的收费方式是________(填“①”或“②”),月租费是________元;
(2)分别求出①,②两种收费方式中y与自变量x之间的函数表达式;
(3)请你根据用户通讯时间的多少,给出经济实惠的选择建议.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是直线AB上任一点,射线OD和射线OE分别平分∠AOC和∠BOC. 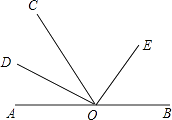
(1)与∠AOE互补的角是 .
(2)若∠AOC=72°,求∠DOE的度数;
(3)当∠AOC=x时,请直接写出∠DOE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题学习】小芸在小组学习时问小娟这样一个问题:已知α为锐角,且sinα=![]() ,求sin2α的值.小娟是这样给小芸讲解的:
,求sin2α的值.小娟是这样给小芸讲解的:
构造如图1所示的图形,在⊙O中,AB是直径,点C在⊙O上,所以∠ACB=90°,作CD⊥AB于D.设∠BAC=α,则sinα=![]() ,可设BC=x,则AB=3x,….
,可设BC=x,则AB=3x,….
【问题解决】
(1)请按照小娟的思路,利用图1求出sin2α的值;(写出完整的解答过程)
(2)如图2,已知点M,N,P为⊙O上的三点,且∠P=β,sinβ=![]() ,求sin2β的值.
,求sin2β的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若a=﹣0.32,b=﹣3﹣2,c=![]() ;d=
;d=![]() ,则它们的大小关系是( )
,则它们的大小关系是( )
A. a<b<c<d B. b<a<d<c C. a<d<c<b D. c<a<d<b
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com