
【题目】某通讯公司推出①,②两种通讯收费方式供用户选择,其中一种有月租费,另一种无月租费,且两种收费方式的通讯时间x(分)与费用y(元)之间的函数关系如图所示.
(1)有月租的收费方式是________(填“①”或“②”),月租费是________元;
(2)分别求出①,②两种收费方式中y与自变量x之间的函数表达式;
(3)请你根据用户通讯时间的多少,给出经济实惠的选择建议.

【答案】(1)① 30;(2)y1=0.1x+30,y2=0.2x;(3)当通话时间少于300分钟时,选择通话方式②实惠;当通话时间超过300分钟时,选择通话方式①实惠;当通话时间为300分钟时,选择通话方式①,②花费一样.
【解析】试题分析:(1)根据当通讯时间为零的时候的函数值可以得到哪种方式有月租,哪种方式没有,有多少;
(2)根据图象经过的点的坐标设出函数的解析式,用待定系数法求函数的解析式即可;
(3)求出当两种收费方式费用相同的时候自变量的值,以此值为界说明消费方式即可.
解:(1)①;30;
(2)设y1=k1x+30,y2=k2x,由题意得:将(500,80),(500,100)分别代入即可:
500k1+30=80,
∴k1=0.1,
500k2=100,
∴k2=0.2
故所求的解析式为y1=0.1x+30; y2=0.2x;
(3)当通讯时间相同时y1=y2,得0.2x=0.1x+30,解得x=300;
当x=300时,y=60.
故由图可知当通话时间在300分钟内,选择通话方式②实惠;
当通话时间超过300分钟时,选择通话方式①实惠;
当通话时间在300分钟时,选择通话方式①、②一样实惠.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,点O是直线AB上任一点,射线OD和射线OE分别平分∠AOC和∠BOC. 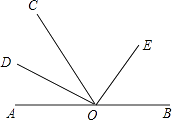
(1)与∠AOE互补的角是 .
(2)若∠AOC=72°,求∠DOE的度数;
(3)当∠AOC=x时,请直接写出∠DOE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+2x+3与x轴交于A、B两点,与y轴交于C点,对称轴与抛物线相交于点M,与x轴相交于点N.点P是线段MN上的一动点,过点P作PE⊥CP交x轴于点E.
(1)直接写出抛物线的顶点M的坐标是 .
(2)当点E与点O(原点)重合时,求点P的坐标.
(3)点P从M运动到N的过程中,求动点E的运动的路径长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们用有理数的运算研究下面问题.规定:水位上升为正,水位下降为负;几天后为正,几天前为负.如果水位每天下降4cm,那么3天后的水位变化用算式表示正确的是( )
A. (+4)×(+3) B. (+4)×(﹣3) C. (﹣4)×(+3) D. (﹣4)×(﹣3)
查看答案和解析>>
科目:初中数学 来源: 题型:
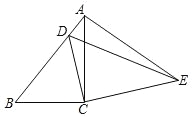
【题目】如图,在△ABC中,∠ACB=90°,AB=9,cosB=![]() ,把△ABC绕着点C旋转,使点B与AB边上的点D重合,点A落在点E,则点A、E之间的距离为 .
,把△ABC绕着点C旋转,使点B与AB边上的点D重合,点A落在点E,则点A、E之间的距离为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com