
【题目】水果店购进某种水果的成本为10元/千克,经市场调研,获得销售单价p(元/千克)与销售时间t(1≤t≤15,t为整数)(天)之间的部分数据如下表:
销售时间t(1≤t≤15,t为整数)(天) | 1 | 4 | 5 | 8 | 12 |
销售单价p(元/千克) | 20.25 | 21 | 21.25 | 22 | 23 |
已知p与t之间的变化规律符合一次函数关系.
(1)试求p关于t的函数表达式;
(2)若该水果的日销量y(千克)与销售时间t(天)的关系满足一次函数y=-2t+120(1≤t≤15,t为整数).
① 求销售过程中最大日销售利润为多少?
② 在实际销售的前12天中,公司决定每销售1千克水果就捐赠n元利润(n<3)给“精准扶贫”对象.现发现:在前12天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围
【答案】(1)p=![]() t+20(1≤t≤15,t为整数);(2)①1250元;②1≤n<3
t+20(1≤t≤15,t为整数);(2)①1250元;②1≤n<3
【解析】
(1)设p=kt+b,利用待定系数法即可解决问题;
(2)日利润=日销售量×每公斤利润,根据函数性质求最大值后比较得结论;
(3)列式表示前12天中每天扣除捐赠后的日销售利润,根据函数性质求n的取值范围.
解:(1)设p与t之间的变化的一次函数关系为:p=kt+b,
将点(4,21)、(8,22)代入上式得:![]() ,解得:
,解得: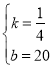 ,
,
故p关于t的函数表达式为:p=![]() t+20(1≤t≤15,t为整数);
t+20(1≤t≤15,t为整数);
(2)①设日销售利润为w,由题意得:
w=y(p-10)=(-2t+120) (![]() t+10)
t+10)
=-![]() t2+10t+1200
t2+10t+1200
=-![]() (t-10)2+1250(1≤t≤15,t为整数),
(t-10)2+1250(1≤t≤15,t为整数),
∵![]() <0,故w有最大值,
<0,故w有最大值,
∴当t=10时,w的最大值为1250;
故销售过程中最大日销售利润为1250元;
②设捐赠后的日销售利润为m,由题意得:
m=w-n=![]() t2+10t+1200-n(-2t+120)
t2+10t+1200-n(-2t+120)
=![]() t2+10t+1200+2nt-120n
t2+10t+1200+2nt-120n
=-![]() t2+(10+2n)t+1200-120n,
t2+(10+2n)t+1200-120n,
∵在前12天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,
∴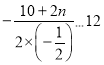 ,
,
∴n≥1.
又∵n<3,
∴n的取值范围为1≤n<3.


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=4,动点P从A点出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,则y关于x的函数图象大致是( )

A. B.
B.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
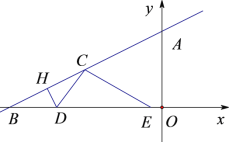
【题目】如图,在平面直角坐标系xOy中,直线![]() 与y轴,x轴分别相交于点A、B.点D是x轴上动点,点D从点B出发向原点O运动,点E在点D右侧,DE=2BD.过点D作DH⊥AB于点H,将△DBH沿直线DH翻折,得到△DCH,连接CE.设BD=t,△DCE与△AOB重合部分面积为S.求:
与y轴,x轴分别相交于点A、B.点D是x轴上动点,点D从点B出发向原点O运动,点E在点D右侧,DE=2BD.过点D作DH⊥AB于点H,将△DBH沿直线DH翻折,得到△DCH,连接CE.设BD=t,△DCE与△AOB重合部分面积为S.求:
(1)求线段BC的长(用含t的代数式表示);
(2)求S关于t的函数解析式,并直接写出自变量t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
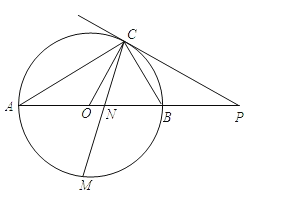
【题目】如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
(1)求证:PC是⊙O的切线;
(2)点M是![]() 的中点,CM交AB于点N,若AB=6,求MNMC的值.
的中点,CM交AB于点N,若AB=6,求MNMC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
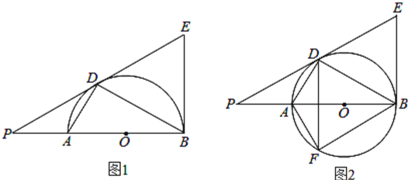
【题目】如图,AB是圆O的直径,O为圆心,AD、BD是半圆的弦,且∠PDA=∠PBD.延长PD交圆的切线BE于点E.
(1)证明:直线PD是⊙O的切线;
(2)如果∠BED=60°,PD=![]() ,求PA的长;
,求PA的长;
(3)将线段PD以直线AD为对称轴作对称线段DF,点F正好在圆O上,如图2,求证:四边形DFBE为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正△ABC的边长为2,以BC边上的高AB1为边作正△AB1C1,△ABC与△AB1C1公共部分的面积记为S1;再以正△AB1C1边B1C1上的高AB2为边作正△AB2C2,△AB1C1与△AB2C2公共部分的面积记为S2;…,以此类推,则Sn=____.(用含n的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC的两条直角边AB=4cm,AC=3cm,点D沿AB从A向B运动,速度是1cm/秒,同时,点E沿BC从B向C运动,速度为2cm/秒. 动点E到达点C时运动终止.连结DE、CD、AE.(1)填空:当动点运动_______ 秒时,△BDE与△ABC相似?
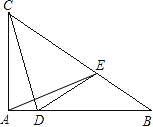
(2)设动点运动t秒时△ADE的面积为s,求s与t的函数解析式;
(3)在运动过程中是否存在某一时刻t,使CD⊥DE?若存在,求出时刻t;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
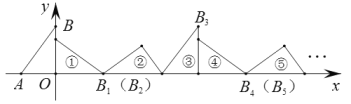
【题目】如图,在平面直角坐标系中,已知点A(-1.5,0),B(0,2),将△ABO顺着x轴的正半轴无滑动的滚动,第一次滚动到①的位置,点B的对应点记作B1;第二次滚动到②的位置,点B1的对应点记作B2;第三次滚动到③的位置,点B2的对应点记作B3;![]() ;依次进行下去,则点B2020的坐标为__________.
;依次进行下去,则点B2020的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
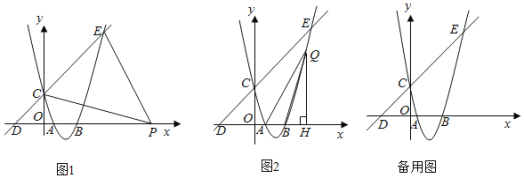
【题目】如图,抛物线y=ax2+bx+c的图象,经过点A(1,0),B(3,0),C(0,3)三点,过点C,D(﹣3,0)的直线与抛物线的另一交点为E.
(1)请你直接写出:
①抛物线的解析式 ;
②直线CD的解析式 ;
③点E的坐标( , );
(2)如图1,若点P是x轴上一动点,连接PC,PE,则当点P位于何处时,可使得∠CPE=45°,请你求出此时点P的坐标;
(3)如图2,若点Q是抛物线上一动点,作QH⊥x轴于H,连接QA,QB,当QB平分∠AQH时,请你直接写出此时点Q的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com