
【题目】如图,Rt△ABC的两条直角边AB=4cm,AC=3cm,点D沿AB从A向B运动,速度是1cm/秒,同时,点E沿BC从B向C运动,速度为2cm/秒. 动点E到达点C时运动终止.连结DE、CD、AE.(1)填空:当动点运动_______ 秒时,△BDE与△ABC相似?
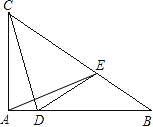
(2)设动点运动t秒时△ADE的面积为s,求s与t的函数解析式;
(3)在运动过程中是否存在某一时刻t,使CD⊥DE?若存在,求出时刻t;若不存在,请说明理由.
【答案】(1)![]() 秒或
秒或![]() 秒;(2)s=
秒;(2)s=![]() t2(0≤t≤
t2(0≤t≤![]() );(3)存在,
);(3)存在,![]() .
.
【解析】
试题设D点运动时间为t,则AD=t,BD=4-t,BE=2t,CE=5-2t(0≤t≤![]() ),
),
(1)分类:当∠BDE=∠BAC,即ED⊥AB时,Rt△BDE∽Rt△BAC;当∠BDE=∠BAC,即DE⊥AB时,Rt△BDE∽Rt△BCA,然后分别根据三角形相似的性质得到比例线段求出t的值;
(2)过E作EF⊥AB于F,易证Rt△BEF∽Rt△BAC,根据三角形相似的性质得到比例线段用t表示EF,BF,然后根据三角形的面积公式求解即可;
(3)先计算出DF=AB-AD-BF,若CD⊥DE,则易证得Rt△ACD∽Rt△FDE,然后根据三角形相似的性质得到比例线段求出t.
试题解析:设D点运动时间为t,则AD=t,BD=4-t,BE=2t,CE=5-2t(0≤t≤![]() ),
),
(1)当∠BDE=∠BAC,即ED⊥AB时,Rt△BDE∽Rt△BAC,
∴BD:BA=BE:BC,即(4-t):4=2t:5,
∴t=![]() ;
;
当∠BDE=∠BAC,即DE⊥AB时,Rt△BDE∽Rt△BCA,
∴BD:BC=BE:BA,即(4-t):5=2t:4,
∴t=![]() ;
;
所以当动点运动![]() 秒或
秒或![]() 秒时,△BDE与△ABC相似;
秒时,△BDE与△ABC相似;
(2)过E作EF⊥AB于F,如图,
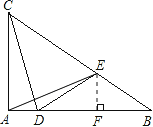
易证Rt△BEF∽Rt△BAC,
∴EF:AC=BF:AB=BE:BC,即EF:3=BF:4=2t:5,
∴EF=![]() ,BF=
,BF=![]() ,
,
∴S=![]() AD×EF=
AD×EF=![]() ×t×
×t×![]() =
=![]() t2(0≤t≤
t2(0≤t≤![]() );
);
(3)存在.
DF=AB-AD-BF=4-t-![]() =4-
=4-![]() t,
t,
若CD⊥DE,
易证得Rt△ACD∽Rt△FDE,
∴AC:DF=AD:EF,即3:(4-![]() t)=t:
t)=t:![]() ,
,
∴t=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
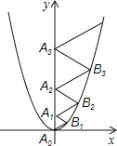
【题目】二次函数y=![]() x2的图象如图所示,点A0位于坐标原点,点A1、A
x2的图象如图所示,点A0位于坐标原点,点A1、A![]() 、A
、A![]() 、…、A
、…、A![]() 在y轴的正半轴上,点B
在y轴的正半轴上,点B![]() 、B
、B![]() 、B
、B![]() 、…、B
、…、B![]() 在二次函数y=
在二次函数y=![]() x2位于第一象限的图象上,若△A0B1A1、△A1B2A2、△A2B3A3、…、△A2017B2018A2018都为等边三角形,则△A
x2位于第一象限的图象上,若△A0B1A1、△A1B2A2、△A2B3A3、…、△A2017B2018A2018都为等边三角形,则△A![]() B
B![]() A
A![]() 的边长=____________.
的边长=____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
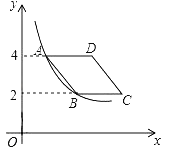
【题目】如图,在平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的纵坐标分别为4,2,反比例函数y=![]() (x>0)的图象经过A,B两点,若菱形ABCD的面积为2
(x>0)的图象经过A,B两点,若菱形ABCD的面积为2![]() ,则k的值为______.
,则k的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果店购进某种水果的成本为10元/千克,经市场调研,获得销售单价p(元/千克)与销售时间t(1≤t≤15,t为整数)(天)之间的部分数据如下表:
销售时间t(1≤t≤15,t为整数)(天) | 1 | 4 | 5 | 8 | 12 |
销售单价p(元/千克) | 20.25 | 21 | 21.25 | 22 | 23 |
已知p与t之间的变化规律符合一次函数关系.
(1)试求p关于t的函数表达式;
(2)若该水果的日销量y(千克)与销售时间t(天)的关系满足一次函数y=-2t+120(1≤t≤15,t为整数).
① 求销售过程中最大日销售利润为多少?
② 在实际销售的前12天中,公司决定每销售1千克水果就捐赠n元利润(n<3)给“精准扶贫”对象.现发现:在前12天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C是弧BE中点,AE⊥CD于点D,延长DC,AB交于点F,已知AD=4,FC=![]() FB.
FB.
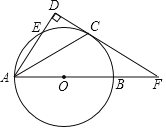
(1)求证:CD是⊙O的切线.
(2)求线段FC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、已两家商场平时以同样价格出售相同的商品,春节期间两家商场都让利酬宾,其中甲商场所有商品按![]() 折出售,乙商场对一次购物中超过200元后的价格部分打
折出售,乙商场对一次购物中超过200元后的价格部分打![]() 折. 设原价购物金额累计为
折. 设原价购物金额累计为![]() 元(
元(![]() ).
).
![]() 根据题意,填写下表: (单位:元)
根据题意,填写下表: (单位:元)
原价购物金额累计/元. | 130 | 300 | 700 | ··· |
甲商场实际购物金额/元 | 104 | 560 | ··· | |
乙商场实际购物金额/元 | 130 | 270 | ··· |
![]() 设在甲商场实际购物金额为
设在甲商场实际购物金额为![]() 元,在乙商场实际购物金额为
元,在乙商场实际购物金额为![]() 元,分别写出
元,分别写出![]() ,
,![]() 关于
关于![]() 的函数解析式;
的函数解析式;
![]() 根据题意填空:
根据题意填空:
①若在同甲商场和在乙商场实际购物花费金额一样多,则在同一商场所购商品原价金额累计为______元 ;
②若在同一商场购物,商品原价购物金额累计为![]() 元,则在甲、乙.两家商场中的 商场实际购物花费金少.
元,则在甲、乙.两家商场中的 商场实际购物花费金少.
③若在同一商场实际购物金额为![]() 元,则在甲、乙两家商场中的_____商场商品原价购物累计金额多.
元,则在甲、乙两家商场中的_____商场商品原价购物累计金额多.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在读书月活动中,学校准备购买一批课外读物.为使课外读物满足同学们的需求,学校就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学只选一类),如图是根
据调查结果绘制的两幅不完整的统计图.

请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了 名同学;
(2)条形统计图中,m= ,n= ;
(3)扇形统计图中,艺术类读物所在扇形的圆心角是 度;
(4)学校计划购买课外读物6000册,请根据样本数据,估计学校购买其他类读物多少册比较合理?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,O为坐标原点,点A(4,0),点B(0,4),C是AB中点,连接OC,将△AOC绕点A顺时针旋转,得到△AMN,记旋转角为α,点O,C的对应点分别是M,N.连接BM,P是BM中点,连接OP,PN.
(Ⅰ)如图①.当α=45°时,求点M的坐标;
(Ⅱ)如图②,当α=180°时,求证:OP=PN且OP⊥PN;
(Ⅲ)当△AOC旋转至点B,M,N共线时,求点M的坐标(直接写出结果即可).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com