
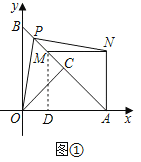
����Ŀ����ֱ������ϵ�У�OΪ����ԭ�㣬��A��4��0������B��0��4����C��AB�е㣬����OC������AOC�Ƶ�A˳ʱ����ת���õ���AMN������ת��Ϊ������O��C�Ķ�Ӧ��ֱ���M��N������BM��P��BM�е㣬����OP��PN��
������ͼ����������45��ʱ�����M�����ꣻ
������ͼ����������180��ʱ����֤��OP��PN��OP��PN��
������AOC��ת����B��M��N����ʱ�����M�����ֱ꣨��д��������ɣ���

���𰸡�����M��4��2![]() ��2
��2![]() ���������������������������ĵ�M������Ϊ��2��2
���������������������������ĵ�M������Ϊ��2��2![]() ����2����2
����2����2![]() ����
����
��������
������ͼ���У�����M��MD��OA��D����ֱ�����������OD��OM���ɽ�����⣮
������ͼ�ڣ�������180��ʱ����B��A��N���ߣ�O��A��M���ߣ�����ֱ��������б�����߶������ɽ�����⣮
�����������Σ�����ͼ��1�У�����M���߶�BN��ʱ������ͼ��2�У�����N���߶�BM��ʱ���ֱ���⼴�ɽ�����⣮
������ͼ���У�����M��MD��OA��D��
��A��4��0����B��0��4����
��OA��OB��4��
��C��AB���е㣬
��OC��CB��CA��![]() AB����OC��AB��
AB����OC��AB��
���AOC�ǵ���ֱ�������Σ�
�൱����45��ʱ����M��AB�ϣ�
����ת��֪����AOC�ա�AMN��
��AM��OA��4��MD��AD��![]() AM��2
AM��2![]() ��
��
��OD��OA��AD��4��2![]() ��
��
��M��4��2![]() ��2
��2![]() ����
����
������ͼ����������180��ʱ����B��A��N���ߣ�O��A��M���ߣ�

�ߡ�BNM����BOM��90�㣬P��BM���е㣬
��OP��PN��PB��PM��
���PMN����PNM����POB����PBO��
�ߡ�NPM��180�㩁2��PMN����BPO��180�㩁2��PBO��
���MPN+��BPO��360�㩁2����PMN+��PBO��
���MPN+��BPO��360�㩁2��45��+��PMO+��PBO����
�ߡ�PMO+��PBO��90�㣬
���MPN+��BPO��90�㣬
���OPN��180�㩁����MPN+��BPO����90�㣬
��OP��PN��
��������ͼ����1�У�����M���߶�BN��ʱ��
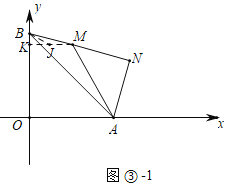
��Rt��ABN����AB��4![]() ��AN��2
��AN��2![]() ��
��
��AB��2AN��
���ABN��30�㣬
��BN��![]() AN��2
AN��2![]() ��BM��BN��MN��2
��BM��BN��MN��2![]() ��2
��2![]() ��
��
����M��MK��OB��K����MK�Ͻ�ȡһ��J��ʹ��BJ��MJ����BK��a��
�ߡ�ABO��45�㣬
���MBK��75�㣬��KMB��15�㣬
��JB��JM��
���JBM����JMB��15�㣬
���BJK����JBM+��JMB��30�㣬
��BJ��JM��2a��KJ��![]() a��
a��
��BM2��BK2+KM2��
�ࣨ2![]() ��2
��2![]() ��2��a2+��2a+
��2��a2+��2a+![]() a��2��
a��2��
���a��4��2![]() �������Ѿ���������
�������Ѿ���������
��KM��2a+![]() a��2��OK��2
a��2��OK��2![]() ��
��
��M��2��2![]() ����
����
����ͼ����2�У�����N���߶�BM��ʱ��ͬ���ɵ�M��2����2![]() ����
����
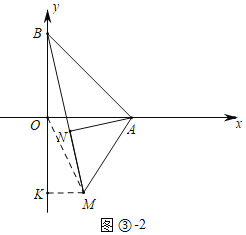
�������������������ĵ�M������Ϊ��2��2![]() ����2����2
����2����2![]() ����
����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
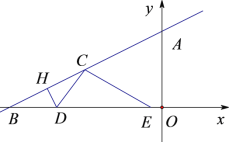
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�ֱ��![]() ��y�ᣬx��ֱ��ཻ�ڵ�A��B����D��x���϶��㣬��D�ӵ�B������ԭ��O�˶�����E�ڵ�D�Ҳ࣬DE=2BD������D��DH��AB�ڵ�H������DBH��ֱ��DH���ۣ��õ���DCH������CE����BD=t����DCE���AOB�غϲ������ΪS����
��y�ᣬx��ֱ��ཻ�ڵ�A��B����D��x���϶��㣬��D�ӵ�B������ԭ��O�˶�����E�ڵ�D�Ҳ࣬DE=2BD������D��DH��AB�ڵ�H������DBH��ֱ��DH���ۣ��õ���DCH������CE����BD=t����DCE���AOB�غϲ������ΪS����
��1�����߶�BC�ij����ú�t�Ĵ���ʽ��ʾ����
��2����S����t�ĺ�������ʽ����ֱ��д���Ա���t��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ABC������ֱ�DZ�AB=4cm��AC=3cm����D��AB��A��B�˶����ٶ���1cm/�룬ͬʱ����E��BC��B��C�˶����ٶ�Ϊ2cm/��. ����E�����Cʱ�˶���ֹ.����DE��CD��AE.��1�����:�������˶�_______ ��ʱ����BDE����ABC���ƣ�
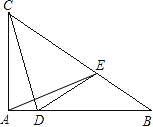
��2���趯���˶�t��ʱ��ADE�����Ϊs����s��t�ĺ�������ʽ��
��3�����˶��������Ƿ����ijһʱ��t��ʹCD��DE�������ڣ����ʱ��t���������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��A(-1.5��0)��B(0��2)������ABO˳��x��������������Ĺ�������һ�ι������ٵ�λ�ã���B�Ķ�Ӧ�����B1���ڶ��ι������ڵ�λ�ã���B1�Ķ�Ӧ�����B2�������ι������۵�λ�ã���B2�Ķ�Ӧ�����B3��![]() �����ν�����ȥ�����B2020������Ϊ__________��
�����ν�����ȥ�����B2020������Ϊ__________��
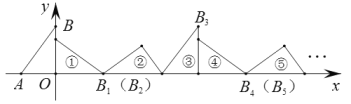
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��ƽ���ı�����������ȫ�ȵ��������Σ�����Ӱ���ֵ������Ϊ![]() ��ƽ���ı��ε������Ϊ
��ƽ���ı��ε������Ϊ![]() ,��
,��![]() ��ֵΪ____��
��ֵΪ____��
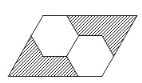
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ������ij�����һ����ѧ����������÷�ȡ����������ͳ�Ʒ����������гɼ��ɵ͵��߷ֳ����飬�����Ƴ���ͼ��ʾ��Ƶ���ֲ�ֱ��ͼ������ֱ��ͼ�ṩ����Ϣ���ش��������⣺
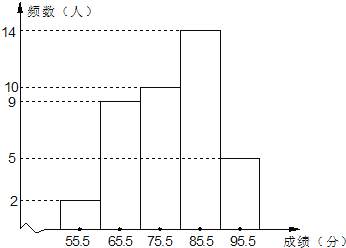
��1���ð����ͬѧ�μ���β��飻
��2����β���ɼ�����λ�����ڵڼ����ڣ�������������
��3������Уһ����360������ѧ���μ���β��飬�ɼ�80�����ϣ�����80�֣�Ϊ���㣬���Ƹ�У�����ѧ��������������Ƕ����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��������x�ύ��A����1��0����B��3��0�����㣬��y�ύ�ڵ�C��0��3����
��1���������ߵĽ���ʽ��
��2����D�ǵ�һ�������������ϵ�һ�����㣨���C��B���غϣ�������D��DF��x���ڵ�F����ֱ��BC�ڵ�E������BD��CD�����D�ĺ�����Ϊm����BCD�����ΪS����S����m�ĺ�������ʽ���Ա���m��ȡֵ��Χ�������S�����ֵ��
��3����֪MΪ�����߶Գ�����һ���㣬����MBC����BCΪֱ�DZߵ�ֱ�������Σ���ֱ��д����M�����꣮
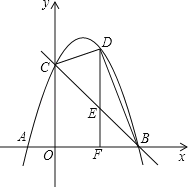
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y��ax2+bx+c��ͼ������A��1��0����B��3��0����C��0��3�����㣬����C��D����3��0����ֱ���������ߵ���һ����ΪE��
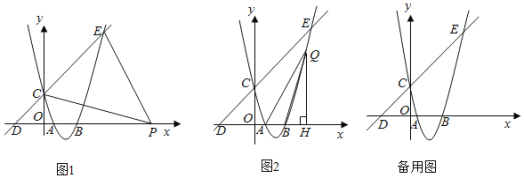
��1������ֱ��д����
�������ߵĽ���ʽ�� ����
��ֱ��CD�Ľ���ʽ�� ����
����E�����꣨�� ������ ������
��2����ͼ1������P��x����һ���㣬����PC��PE����Pλ�ںδ�ʱ����ʹ�á�CPE��45�㣬���������ʱ��P�����ꣻ
��3����ͼ2������Q����������һ���㣬��QH��x����H������QA��QB����QBƽ�֡�AQHʱ������ֱ��д����ʱ��Q�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() Ϊ
Ϊ![]() ��ֱ����
��ֱ����![]() Ϊ
Ϊ![]() �ϲ�ͬ��
�ϲ�ͬ��![]() �����㣬
�����㣬![]() ������
������![]() .����
.����![]() ��
��![]() ������Ϊ
������Ϊ![]() ��ֱ��
��ֱ��![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ��
��
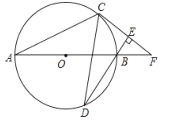
��1����֤��![]() Ϊ
Ϊ![]() �����ߣ�
�����ߣ�
��2����![]() ��
��![]() ʱ����
ʱ����![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com