
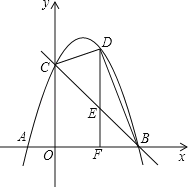
����Ŀ����ͼ����֪��������x�ύ��A����1��0����B��3��0�����㣬��y�ύ�ڵ�C��0��3����
��1���������ߵĽ���ʽ��
��2����D�ǵ�һ�������������ϵ�һ�����㣨���C��B���غϣ�������D��DF��x���ڵ�F����ֱ��BC�ڵ�E������BD��CD�����D�ĺ�����Ϊm����BCD�����ΪS����S����m�ĺ�������ʽ���Ա���m��ȡֵ��Χ�������S�����ֵ��
��3����֪MΪ�����߶Գ�����һ���㣬����MBC����BCΪֱ�DZߵ�ֱ�������Σ���ֱ��д����M�����꣮
���𰸡���1��y����x2+2x+3 ��2��![]() ��
��![]() ��3����1����2������1��4��
��3����1����2������1��4��
��������
��1�������߽���ʽΪy��a��x��1����x3����a��x22x3��������C������뼴����⣻
��2�������ֱ��BC�Ľ���ʽ����D��m����m2+2m+3����E��m����m+3�����õ�DE������m2+2m+3��������m+3������m2+3m��������![]() ��������⣻
��������⣻
��3����MC��б�ߡ�MB��б������������ֱ���⼴�ɣ�
�⣺��1�������߽���ʽΪy��a��x+1����x��3����a��x22x3����
����C�������,��
-3a��3����ã�a��-1��
�����߽���ʽΪy����x2+2x+3��
��2����ֱ��BC�ĺ�������ʽΪy��kx+b��
��ֱ��BC����B��3��0����C��0��3����
��![]() �����
�����![]() ��
��
��y����x+3��
��D��m����m2+2m+3����E��m����m+3����
��DE������m2+2m+3��������m+3������m2+3m��
��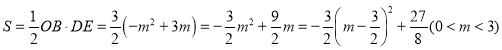 ��
��
��![]() ��
��
����![]() ʱ��S�����ֵ�����ֵ
ʱ��S�����ֵ�����ֵ![]() ��
��
��3��������y����x2+2x+3�ĶԳ���Ϊֱ��x=1
���M��1��m����
��MB2��m2+4��MC2��1+��m��3��2��BC2��18��
����MC��б��ʱ��
1+��m��3��2��m2+4+18��
��ã�m����2��
����MB��б��ʱ��
ͬ���ɵã�m��4��
�ʵ�M������Ϊ����1����2������1��4����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����ABCD�ڵ�һ�����ڣ���BC��x��ƽ�У�A��B�����������ֱ�Ϊ4��2������������y��![]() (x��0)��ͼ��A��B���㣬������ABCD�����Ϊ2
(x��0)��ͼ��A��B���㣬������ABCD�����Ϊ2![]() ����k��ֵΪ______.
����k��ֵΪ______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڶ����»�У�ѧУ������һ��������Ϊʹ�����������ͬѧ�ǵ�����ѧУ�͡�����ϲ���Ŀ���������ѧ�����������պ������ĸ��������˳������飨ÿλͬѧֻѡһ�ࣩ����ͼ�Ǹ�
�ݵ��������Ƶ�������������ͳ��ͼ��

�������ͳ��ͼ�ṩ����Ϣ������������⣺
��1�����ε����У�һ���������� ����ͬѧ��
��2������ͳ��ͼ�У�m=�� ����n=�� ����
��3������ͳ��ͼ�У�����������������ε�Բ�Ľ����� ���ȣ�
��4��ѧУ�ƻ�����������6000�ᣬ������������ݣ�����ѧУ���������������ٲ�ȽϺ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵ�У�OΪ����ԭ�㣬��A��4��0������B��0��4����C��AB�е㣬����OC������AOC�Ƶ�A˳ʱ����ת���õ���AMN������ת��Ϊ������O��C�Ķ�Ӧ��ֱ���M��N������BM��P��BM�е㣬����OP��PN��
������ͼ����������45��ʱ�����M�����ꣻ
������ͼ����������180��ʱ����֤��OP��PN��OP��PN��
������AOC��ת����B��M��N����ʱ�����M�����ֱ꣨��д��������ɣ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
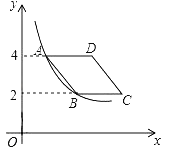
����Ŀ����ͼ��ֱ��y1=3x��5�뷴��������y2=![]() ��ͼ���ཻA��2��m����B��n����6�����㣬����OA��OB��
��ͼ���ཻA��2��m����B��n����6�����㣬����OA��OB��
��1����k��n��ֵ��
��2������AOB�������
��3��ֱ��д��y1�� y2ʱ�Ա���x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC�͡�DEF������ȫ�ȵĵ���ֱ�������Σ���BAC=��EDF=90�㣬��EDF�Ķ���E���ABC��б��BC���е��غϣ�����DEF�Ƶ�E��ת����ת�����У��߶�DE���߶�AB�ཻ�ڵ�P���߶�EF������CA�ཻ�ڵ�Q��
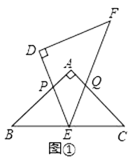
��1����ͼ��������Q���߶�AC�ϣ���AP=AQʱ����֤����BPE�ա�CQE��
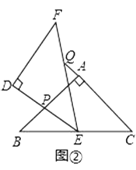
��2����ͼ��������Q���߶�CA���ӳ�����ʱ����֤����BPE�ס�CEQ��
��3���ڣ�2���������£�BP=2��CQ=9����BC�ij�Ϊ_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
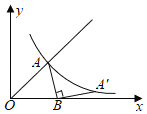
����Ŀ����ͼ������y��x��x��0����ͼ���뷴��������y��![]() ��ͼ���ڵ�A������A�Ƶ�B��
��ͼ���ڵ�A������A�Ƶ�B��![]() ��0��˳ʱ����ת90��õ��ĵ�A'����y��
��0��˳ʱ����ת90��õ��ĵ�A'����y��![]() ��ͼ���ϣ����A������Ϊ_____��
��ͼ���ϣ����A������Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ���ı���ABCD�У�EΪAB�е㣬AF��![]() FD����E��F��AC��G����AG��GC��_____��
FD����E��F��AC��G����AG��GC��_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У���
����![]() ������
������![]() ����ƽ��6����λ���ȣ��õ���
����ƽ��6����λ���ȣ��õ���![]() ��
��
��1��ֱ��д����![]() �����ꣻ
�����ꣻ
��2����������![]() ������
������![]() ����
����![]() ��ֵ��
��ֵ��
��3����������![]() ���߶�
���߶�![]() ����ֻ��һ��������ʱ���������߶��������
����ֻ��һ��������ʱ���������߶��������![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com