
°æƒø°ø»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±ÍœµxOy÷–£¨÷±œþ![]() ”Îy÷·£¨x÷·∑÷±œýΩª”⁄µ„A°¢B£Æµ„D «x÷·…œ∂ص„£¨µ„D¥”µ„B≥ˆ∑¢œÚ‘≠µ„O‘À∂Ø£¨µ„E‘⁄µ„D”“≤ý£¨DE=2BD£Æπ˝µ„D◊˜DH°ÕAB”⁄µ„H£¨Ω´°˜DBH—ÿ÷±œþDH∑≠’€£¨µ√µΩ°˜DCH£¨¡¨Ω”CE£Æ…ËBD=t£¨°˜DCE”ΰ˜AOB÷ÿ∫œ≤ø∑÷√ʪ˝Œ™S£Æ«Û£∫
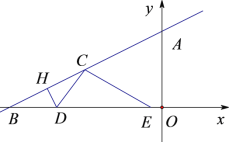
”Îy÷·£¨x÷·∑÷±œýΩª”⁄µ„A°¢B£Æµ„D «x÷·…œ∂ص„£¨µ„D¥”µ„B≥ˆ∑¢œÚ‘≠µ„O‘À∂Ø£¨µ„E‘⁄µ„D”“≤ý£¨DE=2BD£Æπ˝µ„D◊˜DH°ÕAB”⁄µ„H£¨Ω´°˜DBH—ÿ÷±œþDH∑≠’€£¨µ√µΩ°˜DCH£¨¡¨Ω”CE£Æ…ËBD=t£¨°˜DCE”ΰ˜AOB÷ÿ∫œ≤ø∑÷√ʪ˝Œ™S£Æ«Û£∫
£®1£©«Ûœþ∂ŒBCµƒ≥§£®”√∫¨tµƒ¥˙ ˝ Ω±Ì æ£©£ª
£®2£©«ÛSπÿ”⁄tµƒ∫Ø ˝Ω‚Œˆ Ω£¨≤¢÷±Ω”–¥≥ˆ◊‘±‰¡øtµƒ»°÷µ∑∂Œß£Æ
°æ¥∞∏°ø£®1£©![]() £ª£®2£©
£ª£®2£© £Æ
£Æ
°æΩ‚Œˆ°ø
£®1£©œ»«Û≥ˆA,Bµƒ◊¯±Í£¨µ√µΩABµƒ≥§∂»£¨‘Ÿ∏˘æð‘⁄÷±Ω«°˜AOB÷–![]() ,
,![]() £¨¿˚”√”…∑≠’€µ√µΩDB=DC=t£¨BH=CH=
£¨¿˚”√”…∑≠’€µ√µΩDB=DC=t£¨BH=CH=![]() £¨¿˚”√
£¨¿˚”√![]() º¥ø…«ÛΩ‚£ª
º¥ø…«ÛΩ‚£ª
£®2£©∑÷¢Ÿµ„C‘⁄œþ∂ŒAB…œ£¨µ„E‘⁄œþ∂ŒOB…œ£¨¢⁄µ„C‘⁄÷±œþAB…œ£¨µ„E‘⁄œþ∂ŒOB…œ£¨¢€µ„C‘⁄÷±œþAB…œ£¨µ„E‘⁄÷±œþOB…œ£¨∑÷±¿˚”√»˝Ω«∫Ø ˝∫Õ «œýÀ∆»˝Ω«–Œµƒ–‘÷ Ω¯––«ÛΩ‚º¥ø…£Æ
(1)°þ÷±œþ![]() ”Îy÷·£¨x÷·∑÷±œýΩª”⁄µ„A°¢B
”Îy÷·£¨x÷·∑÷±œýΩª”⁄µ„A°¢B
°ýµ„A(0£¨1)£¨B£®-2,0£©
°ý”…π¥π…∂®¿Ìµ√AB=![]()
°ý‘⁄÷±Ω«°˜AOB÷–![]() ,
,![]()

”…∑≠’€÷™
DB=DC=t
BH=CH=![]()
°þ![]()
°ý![]()
°ý![]() £ª
£ª

(2)µ±![]() ±
±
π˝µ„C◊ˆCG°ÕBO”⁄µ„G
°ý![]()
°ý![]()
°ý![]() =
=![]()

µ±![]() ±
±
…ËOAΩªCE”⁄µ„F
°þCD=BD=t£¨![]()
°ý”…π¥π…∂®¿Ìµ√![]()
°ý![]() £¨
£¨![]()
°ý![]()
°þOF°ŒCG
°ý°˜EOF°◊°˜CGE
°ý![]()
°ý![]()
°ý![]() =
=![]() =
=![]()
°ý![]()
=![]() £¨
£¨
…ËCDΩªOA”⁄µ„P
°þOP°ŒCG
°ý°˜DOP°◊DGC
°ý![]()
°þOD=2-t-
°ýOP=![]()
°ý![]() =
=![]()
°ý◊€…œÀ˘ ˆ £Æ
£Æ


 ‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∂˛¥Œ∫Ø ˝y£Ω©Åx2+2x+3£¨Ωÿ»°∏√∫Ø ˝ÕºœÛ‘⁄0°Ðx°Ð4º‰µƒ≤ø∑÷º«Œ™ÕºœÛG£¨…Ëæ≠π˝µ„£®0£¨t£©«“∆Ω––”⁄x÷·µƒ÷±œþŒ™l£¨Ω´ÕºœÛG‘⁄÷±œþlœ¬∑Ωµƒ≤ø∑÷—ÿ÷±œþl∑≠’€£¨ÕºœÛG‘⁄÷±œþ…œ∑Ωµƒ≤ø∑÷≤ª±‰£¨µ√µΩ“ª∏ˆ–¬∫Ø ˝µƒÕºœÛM£¨»Ù∫Ø ˝Mµƒ◊Ó¥Û÷µ”Î◊Ó–°÷µµƒ≤Ó≤ª¥Û”⁄5£¨‘Útµƒ»°÷µ∑∂Œß «£®°°°°£©
A.©Å1°Ðt°Ð0B.©Å1°Ðt![]() C.
C.![]() D.t°Ð©Å1ªÚt°ð0
D.t°Ð©Å1ªÚt°ð0
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
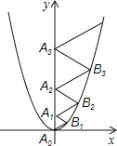
°æƒø°ø∂˛¥Œ∫Ø ˝y£Ω![]() x2µƒÕºœÛ»ÁÕºÀ˘ 棨µ„A0Œª”⁄◊¯±Í‘≠µ„£¨µ„A1°¢A
x2µƒÕºœÛ»ÁÕºÀ˘ 棨µ„A0Œª”⁄◊¯±Í‘≠µ„£¨µ„A1°¢A![]() °¢A
°¢A![]() °¢°≠°¢A
°¢°≠°¢A![]() ‘⁄y÷·µƒ’˝∞Î÷·…œ£¨µ„B
‘⁄y÷·µƒ’˝∞Î÷·…œ£¨µ„B![]() °¢B
°¢B![]() °¢B
°¢B![]() °¢°≠°¢B
°¢°≠°¢B![]() ‘⁄∂˛¥Œ∫Ø ˝y£Ω
‘⁄∂˛¥Œ∫Ø ˝y£Ω![]() x2Œª”⁄µ⁄“ªœÛœÞµƒÕºœÛ…œ£¨»Ù°˜A0B1A1°¢°˜A1B2A2°¢°˜A2B3A3°¢°≠°¢°˜A2017B2018A2018∂ºŒ™µ»±þ»˝Ω«–Œ£¨‘Ú°˜A
x2Œª”⁄µ⁄“ªœÛœÞµƒÕºœÛ…œ£¨»Ù°˜A0B1A1°¢°˜A1B2A2°¢°˜A2B3A3°¢°≠°¢°˜A2017B2018A2018∂ºŒ™µ»±þ»˝Ω«–Œ£¨‘Ú°˜A![]() B
B![]() A
A![]() µƒ±þ≥§£Ω____________£Æ
µƒ±þ≥§£Ω____________£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™£¨‘⁄°˜ABC÷–£¨°œABC£Ω90°„
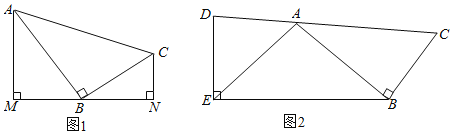
£®1£©»ÁÕº1£¨∑÷±π˝A°¢C¡Ωµ„◊˜æ≠π˝µ„Bµƒ÷±œþMNµƒ¥πœþ£¨¥π◊„∑÷±Œ™M°¢N£Æ
¢Ÿ«Û÷§£∫°˜AMB°◊°˜BNC£ª
¢⁄»Ù°˜AMB°◊°˜ABC£¨«Û÷§£∫AC£ΩAM+CN£ª
£®2£©»ÁÕº2£¨µ„D «CA—”≥§œþ…œµƒ“ªµ„£¨DE°ÕEB£¨AE£ΩAB£¨AD£∫BC£∫CA£Ω3£∫3£∫5£¨«Û![]() µƒ÷µ£Æ
µƒ÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
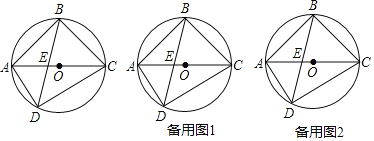
°æƒø°ø»ÁÕº£¨Àƒ±þ–ŒABCDƒ⁄Ω””⁄°—O£¨ACŒ™÷±æ∂£¨AC∫ÕBDΩª”⁄µ„E£¨AB£ΩBC£Æ
£®1£©«Û°œADBµƒ∂» ˝£ª
£®2£©π˝B◊˜ADµƒ∆Ω––œþ£¨ΩªAC”⁄F£¨ ‘≈–∂œœþ∂ŒEA£¨CF£¨EF÷ƺ‰¬˙◊„µƒµ»¡øπÿœµ£¨≤¢Àµ√˜¿Ì”…£ª
£®3£©‘⁄£®2£©Ãıº˛œ¬π˝E£¨F∑÷±◊˜AB£¨BCµƒ¥πœþ£¨¥π◊„∑÷±Œ™G£¨H£¨¡¨Ω”GH£¨ΩªBO”⁄M£¨»ÙAG£Ω3£¨SÀƒ±þ–ŒAGMO£∫SÀƒ±þ–ŒCHMO£Ω8£∫9£¨«Û°—Oµƒ∞Îæ∂£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™£∫»ÁÕº£¨‘⁄![]() ÷–£¨
÷–£¨![]() «AC÷–µ„£¨BE∆Ω∑÷
«AC÷–µ„£¨BE∆Ω∑÷![]() ΩªAC”⁄µ„E£¨µ„O «AB…œ“ªµ„£¨
ΩªAC”⁄µ„E£¨µ„O «AB…œ“ªµ„£¨![]() π˝B°¢E¡Ωµ„£¨ΩªBD”⁄µ„G£¨ΩªAB”⁄µ„
π˝B°¢E¡Ωµ„£¨ΩªBD”⁄µ„G£¨ΩªAB”⁄µ„![]() £¨
£¨![]() ‘Úœ¬√ÊΩ·¬€’˝»∑µƒ”–
‘Úœ¬√ÊΩ·¬€’˝»∑µƒ”–![]() ÃÓ–Ú∫≈
ÃÓ–Ú∫≈![]() ______£®1£©
______£®1£©![]() ”Î
”Î![]() œý«–£ª£®2£©
œý«–£ª£®2£©![]() £ª£®3£©
£ª£®3£©![]() µƒ÷±æ∂µ»”⁄8£ª£®4£©
µƒ÷±æ∂µ»”⁄8£ª£®4£©![]() AE
AE

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
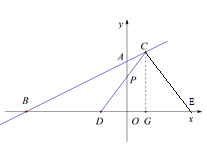
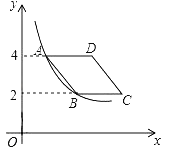
°æƒø°ø»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨¡‚–ŒABCD‘⁄µ⁄“ªœÛœÞƒ⁄£¨±þBC”Îx÷·∆Ω––£¨A£¨B¡Ωµ„µƒ◊ð◊¯±Í∑÷±Œ™4£¨2£¨∑¥±»¿˝∫Ø ˝y£Ω![]() (x£æ0)µƒÕºœÛæ≠π˝A£¨B¡Ωµ„£¨»Ù¡‚–ŒABCDµƒ√ʪ˝Œ™2
(x£æ0)µƒÕºœÛæ≠π˝A£¨B¡Ωµ„£¨»Ù¡‚–ŒABCDµƒ√ʪ˝Œ™2![]() £¨‘Úkµƒ÷µŒ™______.
£¨‘Úkµƒ÷µŒ™______.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øÀÆπ˚µÍπ∫Ω¯ƒ≥÷÷ÀÆπ˚µƒ≥…±æŒ™10‘™/«ßøÀ£¨æ≠ –≥°µ˜—–£¨ªÒµ√œ˙ €µ•º€p£®‘™/«ßøÀ£©”Îœ˙ € ±º‰t£®1°Ðt°Ð15£¨tŒ™’˚ ˝£©£®ÃÏ£©÷ƺ‰µƒ≤ø∑÷ ˝æð»Áœ¬±Ì£∫
œ˙ € ±º‰t£®1°Ðt°Ð15£¨tŒ™’˚ ˝£©£®ÃÏ£© | 1 | 4 | 5 | 8 | 12 |
œ˙ €µ•º€p£®‘™/«ßøÀ£© | 20.25 | 21 | 21.25 | 22 | 23 |
“—÷™p”Ît÷ƺ‰µƒ±‰ªØπʬ…∑˚∫œ“ª¥Œ∫Ø ˝πÿœµ£Æ
£®1£© ‘«Ûpπÿ”⁄tµƒ∫Ø ˝±Ì¥Ô Ω£ª
£®2£©»Ù∏√ÀÆπ˚µƒ»’œ˙¡øy£®«ßøÀ£©”Îœ˙ € ±º‰t£®ÃÏ£©µƒπÿœµ¬˙◊„“ª¥Œ∫Ø ˝y=£≠2t+120£®1°Ðt°Ð15£¨tŒ™’˚ ˝£©£Æ
¢Ÿ «Ûœ˙ €π˝≥Ã÷–◊Ó¥Û»’œ˙ €¿˚»ÛŒ™∂ý…Ÿ£ø
¢⁄ ‘⁄ µº œ˙ €µƒ«∞12ÃÏ÷–£¨π´Àææˆ∂®√øœ˙ €1«ßøÀÀÆπ˚æÕæË‘˘n‘™¿˚»Û£®n£º3£©∏¯°∞æ´◊º∑ˆ∆∂°±∂‘œÛ£Æœ÷∑¢œ÷£∫‘⁄«∞12ÃÏ÷–£¨√øÃÏø€≥˝æË‘˘∫Ûµƒ»’œ˙ €¿˚»ÛÀÊ ±º‰tµƒ‘ˆ¥Û∂¯‘ˆ¥Û£¨«Ûnµƒ»°÷µ∑∂Œß
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄÷±Ω«◊¯±Íœµ÷–£¨OŒ™◊¯±Í‘≠µ„£¨µ„A£®4£¨0£©£¨µ„B£®0£¨4£©£¨C «AB÷–µ„£¨¡¨Ω”OC£¨Ω´°˜AOC»∆µ„AÀ≥ ±’Ζ˝◊™£¨µ√µΩ°˜AMN£¨º«–˝◊™Ω«Œ™¶¡£¨µ„O£¨Cµƒ∂‘”¶µ„∑÷± «M£¨N£Æ¡¨Ω”BM£¨P «BM÷–µ„£¨¡¨Ω”OP£¨PN£Æ
£®¢Ò£©»ÁÕº¢Ÿ£Æµ±¶¡£Ω45°„ ±£¨«Ûµ„Mµƒ◊¯±Í£ª
£®¢Ú£©»ÁÕº¢⁄£¨µ±¶¡£Ω180°„ ±£¨«Û÷§£∫OP£ΩPN«“OP°ÕPN£ª
£®¢Û£©µ±°˜AOC–˝◊™÷¡µ„B£¨M£¨Nπ≤œþ ±£¨«Ûµ„Mµƒ◊¯±Í£®÷±Ω”–¥≥ˆΩ·π˚º¥ø…£©£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com