
【题目】已知,在△ABC中,∠ABC=90°
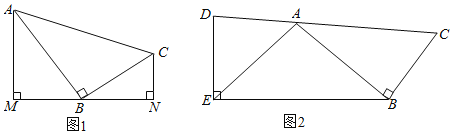
(1)如图1,分别过A、C两点作经过点B的直线MN的垂线,垂足分别为M、N.
①求证:△AMB∽△BNC;
②若△AMB∽△ABC,求证:AC=AM+CN;
(2)如图2,点D是CA延长线上的一点,DE⊥EB,AE=AB,AD:BC:CA=3:3:5,求![]() 的值.
的值.
【答案】(1)①见解析,②见解析;(2)![]()
【解析】
(1)①根据同角的余角相等得到∠BAM=∠CBN,根据两角相等的两个三角形相似证明结论;
②作BH⊥AC,证明△BAM≌△BAH,根据全等三角形的性质得到AH=AM,同理得到CH=CN,证明结论;
(2)过点A作AG⊥BE于G,过点C作CH⊥BE交EB的延长线于H,根据平行线分线段成比例定理得到![]() ,根据△AGB∽△BHC,得到
,根据△AGB∽△BHC,得到![]() ,计算即可.
,计算即可.
(1)①∵∠ABC=90°,
∴∠ABM+∠CBN=90°,
∵AM⊥BM,
∴∠ABM+∠BAM=90°,
∴∠BAM=∠CBN,
∵∠BAM=∠CBN,∠AMB=∠BNC=90°,
∴△AMB∽△BNC;
②如图1,作BH⊥AC于H,
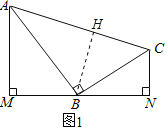
则∠AHB=∠ABC=90°,又∠BAH=∠CAB,
∴△AHB∽△ABC,
∵△AMB∽△ABC,
∴△AMB∽△AHB,
∴∠BAM=∠BAH,
在△BAM和△BAH中,
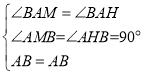 ,
,
∴△BAM≌△BAH(AAS)
∴AH=AM,
同理可证,CH=CN,
∴AC=AH+CH=AM+CN;
(2)如图2,过点A作AG⊥BE于G,过点C作CH⊥BE交EB的延长线于H,
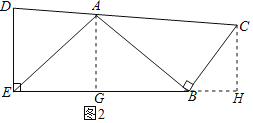
∵∠DEB=90°,
∴CH∥AG∥DE,
∴![]() ,
,
在Rt△ABC中,![]() ,
,
∴![]() ,
,
由(1)①可知,△AGB∽△BHC
∴![]() ,
,
∵AE=AB,AG⊥BE,
∴EG=GB,
∵![]() ,
,
∴EG:BG:BH=3:3:2,
设EG=3a,则BG=3a,BH=2a,
∵![]() ,
,
∴![]() ,
,
解得,![]() ,
,
由勾股定理得,![]() ,
,
∴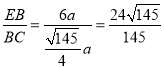 .
.


科目:初中数学 来源: 题型:
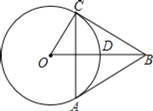
【题目】如图,![]() 的半径为
的半径为![]() 交
交![]() 于点D,点C是
于点D,点C是![]() 上一动点,以BC为边向下作等边
上一动点,以BC为边向下作等边![]() .
.
![]() 当点C运动到
当点C运动到![]() 时,
时,
![]() 求证:BC与
求证:BC与![]() 相切;
相切;
![]() 试判断点A是否在
试判断点A是否在![]() 上,并说明理由.
上,并说明理由.
![]() 设
设![]() 的面积为S,求S的取值范围.
的面积为S,求S的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=4,动点P从A点出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,则y关于x的函数图象大致是( )

A. B.
B.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点.
两点.
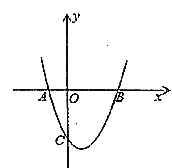
(1)求该抛物线的解析式;
(2)抛物线的对称轴上是否存在一点![]() ,使
,使![]() 的周长最小?若存在,请求出点
的周长最小?若存在,请求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
(3)设抛物线上有一个动点![]() ,当点
,当点![]() 在该抛物线上滑动到什么位置时,满足
在该抛物线上滑动到什么位置时,满足![]() ,并求出此时点
,并求出此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把图1称为一个基本图形,显然这个基本图形中有6个矩形,将此基本图形不断复制并向上平移、叠加,这样得到图2,图3…(如图所示)
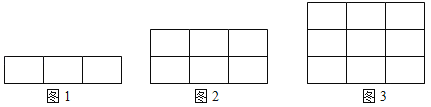
(1)观察图形,完成如表:
图形名称 | 矩形个数 |
图1 | 6 |
图2 | 18 |
图3 | 36 |
图4 | 60 |
图5 |
|
(2)根据以上规律猜想,图形n中共有多少个矩形(用含n的代数式表示)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了维护国家主权和海洋权利,我国海监部门对中国海域实现常态化管理.某日,我国海监船在某海岛附近的海域执行巡逻任务.如图,此时海监船位于海岛P的北偏东30°方向,距离海岛100海里的A处,它沿正南方向航行一段时间后,到达位于海岛P的南偏东45°方向的B处,求海监船航行了多少海里(结果保留根号)?

查看答案和解析>>
科目:初中数学 来源: 题型:
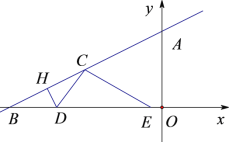
【题目】如图,在平面直角坐标系xOy中,直线![]() 与y轴,x轴分别相交于点A、B.点D是x轴上动点,点D从点B出发向原点O运动,点E在点D右侧,DE=2BD.过点D作DH⊥AB于点H,将△DBH沿直线DH翻折,得到△DCH,连接CE.设BD=t,△DCE与△AOB重合部分面积为S.求:
与y轴,x轴分别相交于点A、B.点D是x轴上动点,点D从点B出发向原点O运动,点E在点D右侧,DE=2BD.过点D作DH⊥AB于点H,将△DBH沿直线DH翻折,得到△DCH,连接CE.设BD=t,△DCE与△AOB重合部分面积为S.求:
(1)求线段BC的长(用含t的代数式表示);
(2)求S关于t的函数解析式,并直接写出自变量t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
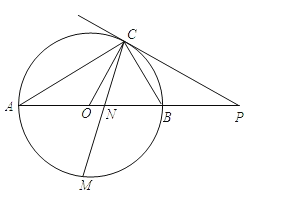
【题目】如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
(1)求证:PC是⊙O的切线;
(2)点M是![]() 的中点,CM交AB于点N,若AB=6,求MNMC的值.
的中点,CM交AB于点N,若AB=6,求MNMC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
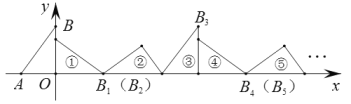
【题目】如图,在平面直角坐标系中,已知点A(-1.5,0),B(0,2),将△ABO顺着x轴的正半轴无滑动的滚动,第一次滚动到①的位置,点B的对应点记作B1;第二次滚动到②的位置,点B1的对应点记作B2;第三次滚动到③的位置,点B2的对应点记作B3;![]() ;依次进行下去,则点B2020的坐标为__________.
;依次进行下去,则点B2020的坐标为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com