
【题目】如图,∠A=∠B=90°,E是AB上的一点,且AE=BC,∠1=∠2.

(1)Rt△ADE与Rt△BEC全等吗?并说明理由;
(2)△CDE是不是直角三角形?并说明理由.
 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:
【题目】一个矩形的长为a,宽为b(a>0,b>0),则矩形的面积为ab.代数式xy(x>0,y>0)可以看作是边长为x和y的矩形的面积.我们可以由此解一元二次方程:x2+x﹣6=0(x>0).具体过程如下:
①方程变形为x(x+1)=6.
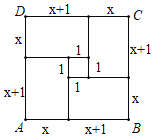
②画四个边长为x+1、x的矩形如图放置;
③由面积关系求解方程.
∵SABCD=(x+x+1)2,又SABCD=4x(x+1)+12.
∴(x+x+1)2=4x(x+1)+1,又x(x+1)=6,
∴(2x+1)2=25,
∵x>0,
∴x=2.
参照上述方法求关于x的二次方程x2+mx﹣n=0的解(x>0,m>0,n>0).(要求:画出示意图,标注相关线段的长度,写出解题步骤)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直角坐标平面上的![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() .若抛物线
.若抛物线![]() 经过
经过![]() 、
、![]() 两点.
两点.

![]() 求
求![]() 、
、![]() 的值;
的值;
![]() 将抛物线向上平移若干个单位得到的新抛物线恰好经过点
将抛物线向上平移若干个单位得到的新抛物线恰好经过点![]() ,求新抛物线的解析式;
,求新抛物线的解析式;
![]() 设
设![]() 中的新抛物的顶点
中的新抛物的顶点![]() 点,
点,![]() 为新抛物线上
为新抛物线上![]() 点至
点至![]() 点之间的一点,以点
点之间的一点,以点![]() 为圆心画图,当
为圆心画图,当![]() 与
与![]() 轴和直线
轴和直线![]() 都相切时,联结
都相切时,联结![]() 、
、![]() ,求四边形
,求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数的图象过点(0,3),且与两坐标轴在第一象限所围成的三角形面积为3,则这个一次函数的表达式为( )
A.y=1.5x+3B.y=1.5x-3C.y=-1.5x+3D.y=-1.5x-3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某洗衣机在洗涤衣服时,经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系如折线图所示,根据图象解答下列问题:
(1)洗衣机的进水时间是______分钟,清洗时洗衣机中的水量是_______升.
(2)进水时y与x之间的关系式是____________.
(3)已知洗衣机的排水速度是每分钟18升,如果排水时间为2分钟,排水结束时洗衣机中剩下的水量是____________升.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图E在△ABC的边AC上,且∠AEB=∠ABC.
⑴求证:∠ABE=∠C;
⑵若∠BAE的平分线AF交BE于F,FD∥BC交AC于D,设AB=5,AC=8,求DC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
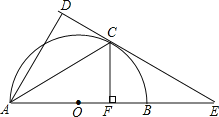
【题目】如图,AB为半圆的直径,O为圆心,C为圆弧上一点,AD垂直于过C点的切线,垂足为D,AB的延长线交直线CD于点E.
(1)求证:AC平分∠DAB;
(2)若BE=2,CE=2![]() ,CF⊥AB,垂足为点F.
,CF⊥AB,垂足为点F.
①求⊙O的半径;②求CF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com