
【题目】如图,![]() 是线段
是线段![]() 、
、![]() 的垂直平分线交点,
的垂直平分线交点,![]() ,
,![]() ,则
,则![]() 的大小是( )
的大小是( )
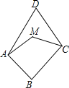
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
过M作射线DN,根据线段垂直平分线的性质得出AM=DM,CM=DM,推出∠DAM=∠ADM,∠DCM=∠CDM,求出∠MAD+∠MCD=∠ADM+∠CDM=∠ADC=65°,根据三角形外角性质求出∠AMC,根据四边形的内角和定理求出即可.
过M作射线DN,如图所示:
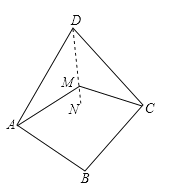
∵M是线段AD、CD的垂直平分线交点,
∴AM=DM,CM=DM,
∴∠DAM=∠ADM,∠DCM=∠CDM,
∴∠MAD+∠MCD=∠ADM+∠CDM=∠ADC,
∵∠ADC=65°,
∴∠MAD+∠MCD=∠ADC=65°,
∴∠AMC=∠AMN+∠CMN=∠DAM+∠ADM+∠DCM+∠CDM=65°+∠ADC=65°+65°=130°
∵AB⊥BC,
∴∠B=90°,
∴∠MAB+∠MCB=360°-∠B-∠AMC=360°-90°-130°=140°,
故选:C.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,二次函数y=﹣![]() x2+bx+c的图象经过A(2,0),B(0,﹣6)两点,
x2+bx+c的图象经过A(2,0),B(0,﹣6)两点,
(1)求这个二次函数的解析式;
(2)设该二次函数的对称轴与x轴交于点C,连接BA,BC,求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(感知)如图,点M是正方形ABCD的边BC上一点,点N是CD延长线上一点,且MA⊥AN,易证△ABM≌△ADN,进而证得∠AMB=∠AND.
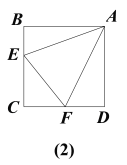
(应用)如图(1),在正方形ABCD中,点E、F分别在边BC、CD上,且∠EAF=45°.求证:∠BEA=∠AEF.
(拓展)如图(2),在四边形ABCD中,AB=AD,∠BAD=90°,∠B+∠D=180°,点E,F分别在边BC、CD上,∠EAF=45°.若∠BEA=50°,则∠AFD的大小为 度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B=90°,E是AB上的一点,且AE=BC,∠1=∠2.

(1)Rt△ADE与Rt△BEC全等吗?并说明理由;
(2)△CDE是不是直角三角形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是半圆
是半圆![]() 的直径,
的直径,![]() 、
、![]() 、
、![]() 是半圆的四等分点,
是半圆的四等分点,![]() 于
于![]() ,连接
,连接![]() 、
、![]() 相交于
相交于![]() 点,连接
点,连接![]() 、
、![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() ,其中正确的结论是( )
,其中正确的结论是( )
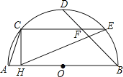
A. ①②③ B. 只有①② C. 只有①③ D. 只有③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有两个纸箱,每个纸箱内各装有4个材质、大小都相同的乒乓球,其中一个纸箱内4个小球上分别写有1、2、3、4这4个数,另一个纸箱内4个小球上分别写有5、6、7、8这4个数,甲、乙两人商定了一个游戏,规则是:从这两个纸箱中各随机摸出一个小球,然后把两个小球上的数字相乘,若得到的积是2的倍数,则甲得1分,若得到积是3的倍数,则乙得2分.完成一次游戏后,将球分别放回各自的纸箱,摇匀后进行下一次游戏,最后得分高者胜出.。
(1)请你通过列表(或树状图)分别计算乘积是2的倍数和3的倍数的概率;
(2)你认为这个游戏公平吗?为什么?若你认为不公平,请你修改得分规则,使游戏对双方公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店准备购进一批电冰箱和空调,每台电冰箱的进价比每台空调的进价多400元,商店用8000元购进电冰箱的数量与用6400元购进空调的数量相等.
(1)求每台电冰箱与空调的进价分别是多少?
(2)已知电冰箱的销售价为每台2100元,空调的销售价为每台1750元.若商店准备购进这两种家电共100台,其中购进电冰箱x台(33≤x≤40),那么该商店要获得最大利润应如何进货?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com