
【题目】如图,![]() 是半圆
是半圆![]() 的直径,
的直径,![]() 、
、![]() 、
、![]() 是半圆的四等分点,
是半圆的四等分点,![]() 于
于![]() ,连接
,连接![]() 、
、![]() 相交于
相交于![]() 点,连接
点,连接![]() 、
、![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() ,其中正确的结论是( )
,其中正确的结论是( )
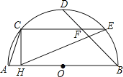
A. ①②③ B. 只有①② C. 只有①③ D. 只有③
【答案】C
【解析】
连结OC、BC、OD,OD交CE于G,如图,由于C、D、E是半圆的四等分点,根据垂径定理得到OD⊥CE,CE=2CG,根据圆心角、弧、弦的关系得到∠AOC=∠COD=45°,根据圆周角定理得∠BCE=∠ABC,再证明四边形CHOG为正方形,则CH=CG,所以CE=2CH;利用等角的余角相等得∠ACH=∠ABC,而∠CEH所对的弧大于AC弧,则∠CEH>∠ABC,所以∠ACH<∠CEH;利用CE∥AB得到∠CFD=∠ABD,而∠ABD=2∠ABC=2∠ACH,于是有∠CFD=2∠ACH.
连结OC、BC、OD,OD交CE于G,如图:
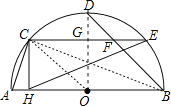
∵C、D、E是半圆的四等分点,
∴OD⊥CE,∠AOC=∠COD=45°,∠BCE=∠ABC,
∴CE=2CG,CE∥AB
∵CH⊥AB,
∴四边形CHOG为正方形,
∴CH=CG,
∴CE=2CH,所以①正确;
∵AB为直径,
∴∠ACB=90°,
∴∠ACH=∠ABC,
而∠CEH所对的弧大于AC弧,
∴∠CEH>∠ABC,
∴∠ACH<∠CEH,所以②错误;
∵CE∥AB,
∴∠CFD=∠ABD,
∵弧AC=弧CD,
∴∠ACB=∠CBD,
∴∠ABD=2∠ABC=2∠ACH,
∴∠CFD=2∠ACH,所以③正确.
故选:C.


科目:初中数学 来源: 题型:
【题目】如图,点A,B,C均在坐标轴上,AO=BO=CO=1,过A,O,C作⊙D,E是⊙D上任意一点,连结CE, BE,则![]() 的最大值是( )
的最大值是( )

A. 4 B. 5 C. 6 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数的图象过点(0,3),且与两坐标轴在第一象限所围成的三角形面积为3,则这个一次函数的表达式为( )
A.y=1.5x+3B.y=1.5x-3C.y=-1.5x+3D.y=-1.5x-3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=4,AC=6,∠ABC和∠ACB的平分线交于O点,过点O作BC的平行线交AB于M点,交AC于N点,则△AMN的周长为( )
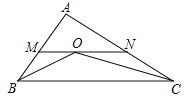
A. 7 B. 8 C. 9 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图E在△ABC的边AC上,且∠AEB=∠ABC.
⑴求证:∠ABE=∠C;
⑵若∠BAE的平分线AF交BE于F,FD∥BC交AC于D,设AB=5,AC=8,求DC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正三角形OAB的顶点B的坐标为(0,2),点A在第一象限内,将△OAB沿直线OA的方向平移至△O′A′B′的位置,此时点A′的横坐标为3![]() ,则点B′的坐标为( )
,则点B′的坐标为( )

A. (2![]() ,4) B. (2
,4) B. (2![]() ,3) C. (3
,3) C. (3![]() ,4) D. (3
,4) D. (3![]() ,3)
,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂生产部门为了解本部门工人的生产能力情况,进行了抽样调查.该部门随机抽取了30名工人某天每人加工零件的个数,数据如下:
20 | 21 | 19 | 16 | 27 | 18 | 31 | 29 | 21 | 22 |
25 | 20 | 19 | 22 | 35 | 33 | 19 | 17 | 18 | 29 |
18 | 35 | 22 | 15 | 18 | 18 | 31 | 31 | 19 | 22 |
整理上面数据,得到条形统计图:
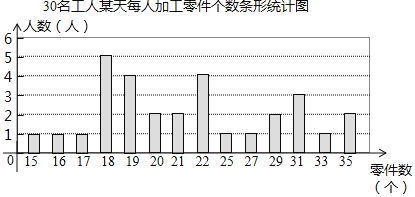
样本数据的平均数、众数、中位数如下表所示:
统计量 | 平均数 | 众数 | 中位数 |
数值 | 23 | m | 21 |
根据以上信息,解答下列问题:
(1)上表中众数m的值为 ;
(2)为调动工人的积极性,该部门根据工人每天加工零件的个数制定了奖励标准,凡达到或超过这个标准的工人将获得奖励.如果想让一半左右的工人能获奖,应根据 来确定奖励标准比较合适.(填“平均数”、“众数”或“中位数”)
(3)该部门规定:每天加工零件的个数达到或超过25个的工人为生产能手.若该部门有300名工人,试估计该部门生产能手的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com