解:(1)∵∠ACB=90°,
∴DC⊥AC.
∵AD平分∠BAC,DE⊥AB,
∴CD=DE,∠DEB=90°.
∴∠EDB+∠B=90°,∠FCD=∠BED.
∵∠CAB+∠B=90°,
∴∠EDB=∠BAC.
∵∠FDC=∠CAB,
∴∠EDB=∠FDC.
∵在△FCD和△BED中,
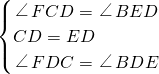
,
∴△FCD≌△BED(SAS),
∴FC=BE;
(2)∵在△GCD和△BED中,
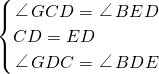
,
∴△GCD≌△BED(ASA),
∴GD=BD,CG=BE,
∴GC=FC=

FG=4,
∴BE=4
∵CD=3,
∴DE=3.
在Rt△GDC中,由勾股定理,得
GD=5,
∴BD=5,
∴BC=8.
∵∠B=∠B,∠BDE=∠BAC,
∴△BDE∽△BAC,
∴
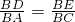
,
∴
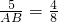
,
∴AB=10.
答:AB的长是10.
分析:(1)根据条件,AD平分∠BAC,DE⊥AB可以得出CD=DE,∠BDE=∠CDF,可以得出△FCD≌△BED,从而得出结论;
(2)根据条件可以得出∠FDC=∠GDC,进而得出∠FDC=∠GDC,得出△FDC≌△GDC,得出FC=GC,由条件可以求出CG的值,根据勾股定理可以求出GD的值,进而得出BD的值,再由△BED∽△BCA,由其性质就可以求出AB的值.
点评:本题考查了角平分线的性质的运用,三角形全等的判定及性质的运用,勾股定理的运用及相似三角形的判定及性质的运用,解答第一问时证明三角形全等是关键,第二问时证明三角形相似是求值的关键.

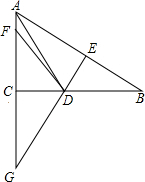
 如图,△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB交AB于点E,点F是AC上一点,∠FDC=∠CAB.
如图,△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB交AB于点E,点F是AC上一点,∠FDC=∠CAB.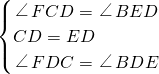 ,
,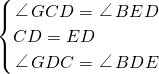 ,
, FG=4,
FG=4,
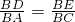 ,
,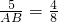 ,
,

 已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.
已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.