
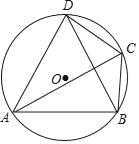
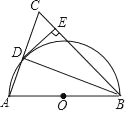
【题目】如图,在⊙O的内接四边形ABCD中,∠BCD=120°,CA平分∠BCD.
(1)求证:△ABD是等边三角形;
(2)若BD=3,求⊙O的半径.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)因为AC平分∠BCD,∠BCD=120°,根据角平分线的定义得:∠ACD=∠ACB=60°,根据同弧所对的圆周角相等,得∠ACD=∠ABD,∠ACB=∠ADB,∠ABD=∠ADB=60°.根据三个角是60°的三角形是等边三角形得△ABD是等边三角形.(2)作直径DE,连结BE,由于△ABD是等边三角形,则∠BAD=60°,由同弧所对的圆周角相等,得∠BED=∠BAD=60°.根据直径所对的圆周角是直角得,∠EBD=90°,则∠EDB=30°,进而得到DE=2BE.设EB=x,则ED=2x,根据勾股定理列方程求解即可.
解:(1)∵∠BCD=120°,CA平分∠BCD,
∴∠ACD=∠ACB=60°,
由圆周角定理得,∠ADB=∠ACB=60°,∠ABD=∠ACD=60°,
∴△ABD是等边三角形;
(2)连接OB、OD,作OH⊥BD于H,
则DH=![]() BD=
BD=![]() ,
,
∠BOD=2∠BAD=120°,
∴∠DOH=60°,
在Rt△ODH中,OD=![]() =
=![]() ,
,
∴⊙O的半径为![]() .
.


科目:初中数学 来源: 题型:
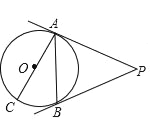
【题目】如图,AC是⊙O的直径,PA切⊙O于点A,点B是⊙O上的一点,且∠BAC=30°,∠APB=60°.
(1)求证:PB是⊙O的切线;
(2)若⊙O的半径为2,求弦AB及PA,PB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校运动会需购买A,B两种奖品,若购买A种奖品3件和B种奖品2件,共需60元;若购买A种奖品5件和B种奖品3件,共需95元.
(1)求A、B两种奖品的单价各是多少元?
(2)学校计划购买A、B两种奖品共100件,购买费用不超过1150元,且A种奖品的数量不大于B种奖品数量的3倍,设购买A种奖品m件,购买费用为W元,写出W(元)与m(件)之间的函数关系式.求出自变量m的取值范围,并确定最少费用W的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
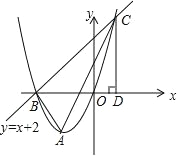
【题目】如图,已知抛物线 y=x2+2x 的顶点为 A,直线 y=x+2 与抛物线交于 B,C 两点.
(1)求 A,B,C 三点的坐标;
(2)作 CD⊥x 轴于点 D,求证:△ODC∽△ABC;
(3)若点 P 为抛物线上的一个动点,过点 P 作 PM⊥x 轴于点 M,则是否还存在除 C 点外的其他位置的点,使以 O,P,M 为顶点的三角形与△ABC 相似? 若存在,请求出这样的 P 点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
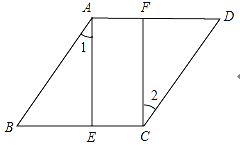
【题目】如图,点E,F在菱形ABCD的对边上,AE⊥BC.∠1=∠2.
(1)判断四边形AECF的形状,并证明你的结论.
(2)若AE=4,AF=2,试求菱形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年,重庆市南岸区广阳镇一果农李灿收获枇杷20吨,桃子12吨,现计划租用甲、乙两种货车共8辆将这批水果全部运往外地销售,已知一辆甲种货车可装枇杷4吨和桃子1吨,一辆乙种货车可装枇杷和桃子各2吨.李灿安排甲、乙两种货车一次性地将水果运到销售地的方案数有( )
A.1种B.2种C.3种D.4种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BA=BC,以AB为直径作⊙O,交AC于点D,连接DB,过点D作DE⊥BC,垂足为E.
(1)求证:AD=CD.
(2)求证:DE为⊙O的切线.
(3)若∠C=60°,DE=![]() ,求⊙O半径的长.
,求⊙O半径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是一块锐角三角形材料,高线AH长8 cm,底边BC长10 cm,要把它加工成一个矩形零件,使矩形DEFG的一边EF在BC上,其余两个顶点D,G分别在AB,AC上,则四边形DEFG的最大面积为( )

A. 40 cm2 B. 20 cm2
C. 25 cm2 D. 10 cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,给出下列结论:
①b2=4ac;②abc>0;③a>c;④4a﹣2b+c>0,其中正确的个数有( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com