
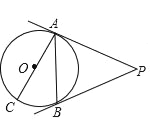
【题目】如图,AC是⊙O的直径,PA切⊙O于点A,点B是⊙O上的一点,且∠BAC=30°,∠APB=60°.
(1)求证:PB是⊙O的切线;
(2)若⊙O的半径为2,求弦AB及PA,PB的长.
【答案】(1)见解析;(2)2
【解析】
试题(1)连接OB,证PB⊥OB.根据四边形的内角和为360°,结合已知条件可得∠OBP=90°得证;
(2)连接OP,根据切线长定理得直角三角形,根据含30度角的直角三角形的性质即可求得结果。
(1)连接OB.
∵OA=OB,∴∠OBA=∠BAC=30°.
∴∠AOB=80°-30°-30°=20°.
∵PA切⊙O于点A,∴OA⊥PA,
∴∠OAP=90°.
∵四边形的内角和为360°,
∴∠OBP=360°-90°-60°-20°=90°.
∴OB⊥PB.
又∵点B是⊙O上的一点,
∴PB是⊙O的切线.
(2)连接OP,
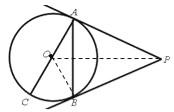
∵PA、PB是⊙O的切线,
∴PA=PB,∠OPA=∠OPB=![]() ,∠APB=30°.
,∠APB=30°.
在Rt△OAP中,∠OAP=90°,∠OPA=30°,
∴OP=2OA=2×2=4.
∴PA=OP2-OA2=2
∵PA=PB,∠APB=60°,
∴PA=PB=AB=2。


科目:初中数学 来源: 题型:
【题目】在四边形 ABCD 中,对角线 AC、BD 相交于点 O,过点 O 的两条直线分别交边 AB、CD、AD、BC 于点 E、F、G、H.
(感知)如图①,若四边形 ABCD 是正方形,且 AG=BE=CH=DF,则 S 四边形AEOG= S 正方形 ABCD;
(拓展)如图②,若四边形 ABCD 是矩形,且 S 四边形 AEOG=![]() S 矩形 ABCD,设 AB=a, AD=b,BE=m,求 AG 的长(用含 a、b、m 的代数式表示);
S 矩形 ABCD,设 AB=a, AD=b,BE=m,求 AG 的长(用含 a、b、m 的代数式表示);
(探究)如图③,若四边形 ABCD 是平行四边形,且 AB=3,AD=5,BE=1, 试确定 F、G、H 的位置,使直线 EF、GH 把四边形 ABCD 的面积四等分.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,CD⊥BC,BD与AC相交于点E,AB=9,BC=4,DC=3.
(1)求BE的长度;
(2)求△ABE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
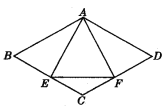
【题目】已知:如图所示,菱形ABCD中,E,F分别是CB,CD上的点,且BE=DF.
(1)试说明:AE=AF;
(2)若∠B=60°,点E,F分别为BC和CD的中点,试说明:△AEF为等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DEF中,已有条件AB=DE,还需要添加两个条件才能使△ABC≌△DEF.不能添加的一组条件是( )

A. ∠B=∠E,BC=EF B. ∠A=∠D,BC=EF
C. ∠A=∠D,∠B=∠E D. BC=EF,AC=DF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在Rt△ABC中,∠C=90°,AB=5cm,AC=3cm,动点P从点B出发沿射线BC以1cm/s的速度移动,设运动的时间为t秒.

(1)求BC边的长;
(2)当△ABP为直角三角形时,求t的值;
(3)当△ABP为等腰三角形时,求t的值
查看答案和解析>>
科目:初中数学 来源: 题型:
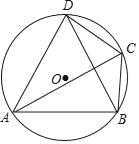
【题目】如图,在⊙O的内接四边形ABCD中,∠BCD=120°,CA平分∠BCD.
(1)求证:△ABD是等边三角形;
(2)若BD=3,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com